Контрольная работа: Решение задачи о 8 ферзях

Цель работы: разработать программу, которая бы наглядно продемонстрировала варианты размещения ферзей на шахматной доске, удовлетворяя правилам задачи.

Метод исследования: изучение литературы, составление и отладка программ на компьютере, проверка решений.

Программа размещения ферзей на практике может применяться в в образовательных целях. Также ее можно использовать для изучения математической модели поставленной задачи. Ведь задача особенно интересна, при увеличении размера шахматной доски.

Задача звучит следующим образом:

«Какими способами можно расставить на доске восемь ферзей так, чтобы они не угрожали друг другу, т.е. никакие два не стояли на одной вертикали, горизонтали и диагонали и сколько таких способов?»

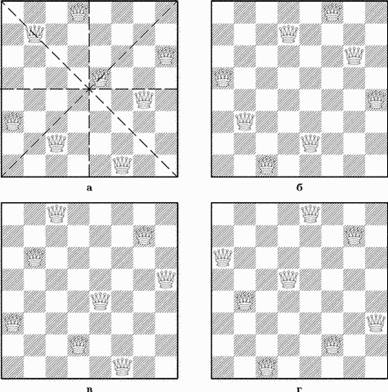
Задача о восьми ферзях

Очевидно, больше восьми мирных ферзей (как и ладей) на обычной доске расставить невозможно. Найти какое-нибудь расположение восьми ферзей, не угрожающих друг другу, легко (на рисунке представлены четыре искомые расстановки). Значительно труднее подсчитать общее число расстановок и вывести их, в чем, собственно, и состоит задача.

Любопытно, что многие авторы ошибочно приписывали эту задачу и ее решение самому К. Гауссу. На самом деле, она была впервые поставлена в 1848 г. немецким шахматистом М. Беццелем. Доктор Ф. Наук нашел 60 решений и опубликовал их в газете «Illustrierte Zeitung» от 1 июня 1850 г. Лишь после этого Гаусс заинтересовался задачей и нашел 72 решения, которые он сообщил в письме к своему другу астроному Шумахеру от 2 сентября 1850 г. Полный же набор решений, состоящий из 92 позиций, получил все тот же Ф. Наук. Он привел их в упомянутой газете от 21 сентября 1850 г. Эта хронология установлена известным немецким исследователем математических развлечений В. Аренсом.

Строгое доказательство того, что 92 решения исчерпывают все возможности, было получено лишь в 1874 г. английским математиком Д. Глэшером (при помощи теории определителей). Забегая вперед, отметим, что существенных решений (не совпадающих при отражениях и поворотах доски) имеется только двенадцать.

Известно много способов организовать эффективный поиск расположения восьми мирных ферзей (методы Пермантье, Ла-Ное, Гюнтера, Глэшера, Лакьера и др.). Эти способы описаны в многочисленной литературе по занимательной математике. В наш век ЭВМ задача такого сорта не вызвала бы столь живой интерес. Ведь достаточно составить несложную программу, и уже через несколько минут после ее введения в машину все 92 необходимые позиции будут выданы на печать.

Из каждого решения задачи о ферзях можно получить ряд других при помощи поворотов (вращений) доски на 90, 180 и 270°, а также при ее зеркальном отражении относительно линий, разделяющих доску пополам. Например, из расстановки, показанной на рис. а, при повороте доски на 90° по часовой стрелке мы получаем расстановку на рис. в, а при отражении доски относительно линии, разделяющей королевский и ферзевый фланги, – на рис. г. При помощи других поворотов и отражений доски можно получить еще пять решений.

Итак, указанные операции с шахматной доской позволяют из одного расположения мирных ферзей получить, вообще говоря, семь новых. Доказано, что в общем случае на доске nхn (при n > 1) для любой расстановки n мирных ферзей возможны три ситуации:

1) при одном отражении доски возникает новая расстановка ферзей, а при поворотах и других отражениях новых решений не получается;

2) новое решение возникает при повороте доски на 90°, а ее отражения дают еще две расстановки;

3) три поворота доски и четыре отражения приводят к семи различным расстановкам (а если считать и исходную, то всего имеем восемь позиций).

В случае 1) исходное решение называется дважды симметрическим, в случае 2) – симметрическим, а в случае 3) – простым. Для обычной доски каждое решение является либо простым, либо симметрическим, а дважды симметрических не существует.

Набор расстановок восьми мирных ферзей называется основным, если, во-первых, эти расстановки не переходят друг в друга при поворотах и отражениях доски, и, во-вторых, любая другая расстановка получается из какой-нибудь основной при помощи данных преобразований доски. Доказано, что всякий основной набор решений задачи содержит ровно 12 расстановок. Вот один из таких наборов:

1) см. рис. а;

2) см. рис. б;

3) a4, b1, c5, d8, e6, f3, g7, h2;

4) a4, b2, c5, d8, e6, f1, g3, h7;

5) a4, b2, c7, d3, e6, f8, g1, h5;

6) a4, b2, c7, d3, e6, f8, g5, h1;

7) a3, b5, c2, d8, e6, f4, g7, h1;

8) a4, b1, c5, d8, e2, f7, g3, h6;

9) a4, b7, c3, d8, e2, f5, g1, h6;

10) a6, b4, c2, d8, e5, f7, g1, h3;

11) a4, b8, c1, d5, e7, f2, g6, h3;

--> ЧИТАТЬ ПОЛНОСТЬЮ <--