Контрольная работа: Самообучающиеся системы

где

y_j – значение выхода j -го нейрона;

S_j – взвешенная сумма входных сигналов j -го нейрона;

w_ij – i -тый вход j – того нейрона.

При этом производная взвешенной суммы по весам будет равна:

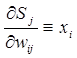
где x_i – значение i -го входа нейрона.

Для выходного слоя производная функции ошибки будет равна:

,

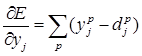где p – номер обучающего образца.

Если в качестве активационной функции используется сигмоид, то будет определяться формулой:

,

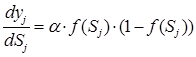где 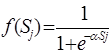, определяет текущее значение выходного сигнала.

Расчеты по вышеприведенным формулам позволяют выполнить коррекцию весов для нейронов последнего слоя. Для получения формул для других слоев можно воспользоваться формулой производной функции ошибки по входному сигналу (n – номер слоя):

.

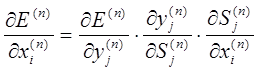Последний сомножитель тождественно совпадает с весовым коэффициентом i – того входа j – того нейрона:

.

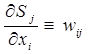Но производная по входному значению для последнего слоя тождественно совпадает с производной по соответствующему выходу для предыдущего слоя:

.

Первый множитель формулы (7) определяется формулой:

,

где k – число нейронов в слое n.

Вводится вспомогательная переменная

Тогда можно задать рекурсивную формулу для определения (n-1) - го слоя, если известны следующего n - го слоя.

.

Нахождение же для последнего слоя нейронной сети не представляет трудности, так как известен целевой вектор, т. е. вектор тех значений, которые должна выдавать нейронная сеть при данном наборе входных значений.

.

Можно записать формулу для приращений весовых коэффициентов в раскрытом виде