Контрольная работа: Симплекс метод решения задачи линейного программирования

Отношение,

θ

i Базис 1 10 8 1 1 0 - 0 ______ 2 16 20 0 1 - 0 ______ 3 0 96 0 0 - 1 ______ ∆j 400 5 0 0 0 Zj 400 14 10 16 0

Так как нет отрицательных оценок ∆j, значит выполняется признак оптимальности и не вводились искусственные переменные, то получено оптимальное решение.

Ответ:

Максимальное значение функции F_max =400 достигается в точке с координатами:

=0

=8

=20

=0

=0

=96

Задача №2 (Метод Литтла)

Найти кратчайший путь в графе, заданном графически в виде чертежа, методом Литтла.

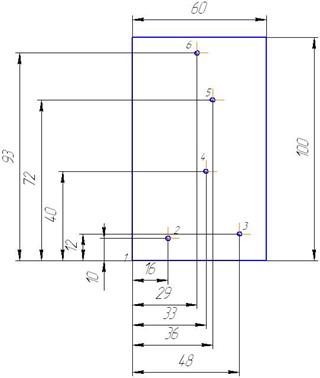
Из чертежа запишем матрицу расстояний. (Расстояние от т.1 до т.2 равно:

, и т.д.)

1	2	3	4	5	6
1	∞	18,87	49,48	51,86	80,51	97,42
2	18,87	∞	32,06	34,48	65,15	84,01
3	49,48	32,06	∞	31,76	61,19	83,20
4	51,86	34,48	31,76	∞	32,14	53,15
5	80,51	65,15	61,19	32,14	∞	22,14
6	97,42	84,01	83,20	53,15	22,14	∞

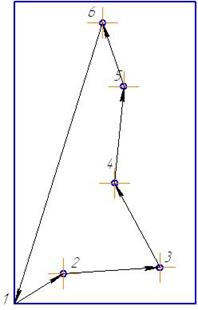
Предположим что кратчайший путь будет следующим:

т.1→ т.2→ т.3→ т.4→ т.5→ т.6→т.1 и составит

Решение: Первый этап.

Шаг 1. Приведем матрицу расстояний по строкам и столбцам

(в строке вычитаем из каждого элемента минимальный, затем в столбцах)

1	2	3	4	5	6
1	∞	18,87	49,48	51,86	80,51	97,42	18,87
2	18,87	∞	32,06	34,48	65,15	84,01	18,87
3	49,48	32,06	∞	31,76	61,19	83,20	31,76
4	51,86	34,48	31,76	∞	32,14	53,15	31,76
5	80,51	65,15	61,19	32,14	∞	22,14	22,14
6	97,42	84,01	83,20	53,15	22,14	∞	22,14

↓

1	2	3	4	5	6
1	∞	0	30,61	32,99	61,64	78,55
2	0	∞	13,19	15,61	46,28	65,14
3	17,72	0,30	∞	0	29,43	51,44
4	20,10	2,72	0	∞	0,38	21,39
5	58,37	43,01	39,05	10,00	∞	0
6	75,28	61,87	61,06	31,01	0	∞
0	0	0	0	0	0

↓

1	2	3	4	5	6
1	∞	0	30,61	32,99	61,64	78,55
2	0	∞	13,19	15,61	46,28	65,14
3	17,72	0,30	∞	0	29,43	51,44
4	20,10	2,72	0	∞	0,38	21,39
5	58,37	43,01	39,05	10,00	∞	0
6	75,28	61,87	61,06	31,01	0	∞

Шаг 2. Определим оценки нулевых клеток:

Шаг 3. Вычеркиваем клетку с максимальной оценкой. Включаем данную клетку в путь обхода. (5 – 6)