Контрольная работа: Статистическое изучение взаимосвязей
0,30
3,09
4
0,773
0,32
2,02
5
0,404
Итого
16,58
20
0,829
Сравнив средние значения результирующего признака по группам можно также сделать вывод, что рост средней занятости рабочего места влечет за собой снижение величины межоперационных перерывов, т.е. можно сказать имеет место обратная корреляционная связь.
Если бы связи между факторными и результативными признакам не было, то все групповые средние были бы приблизительно одинаковы по величине. Оценка существенности расхождения групповых средних лежит в основе использования метода дисперсионного анализа для выявления наличия и оценки связи.
Для предварительного выявления связи и раскрытия ее характера применяют графический метод. Используя данные таблицы 1 построить точечный график, который называют поле корреляции .
Нанеся данные таблицы 3 и соединяя последовательно отрезками прямых соответствующих им точек, получим эмпирическую линию связи.
Если эмпирическая линия приближается к прямой, - предполагают наличие прямолинейной корреляционной связи, если к какой либо кривой, то это может быть связано с наличием криволинейной корреляционной связи.
3. Измерение степени тесноты корреляционной связи между двумя признаками
Показатели тесноты связи дают возможность охарактеризовать степень зависимости вариации результативного признака от вариации признака - фактора.
Зная показатели тесноты корреляционной связи можно ответить на следующие группы вопросов.
1. о необходимости изучения данной связи между признаками и целесообразности ее практического применения;
2. о степени различий тесноты связи в ее проявлении для конкретных условий;
3. сопоставляя показатели тесноты связи результативного признака с различными факторами, можно выявить те факторы, которые в данных конкретных условиях являются решающими.
К простейшим показателям тесноты связи относится коэффициент корреляции знаков (коэффициент Г. Фехнера), основанный на оценке степени согласованности направлений отклонений индивидуальных значений факторного и результативного признаков от соответствующей средней.
Если обозначить 
- число совпадений знаков отклонений индивидуальных величин от средней, 
- число несовпадений, тогда коэффициент Фехнера будет иметь вид:
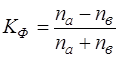
Если знаки всех отклонений совпадут то 
и 
- свидетельствует о наличие прямой связи, если все знаки не совпадают, тогда 
и 
- наличие обратной связи.
Рассмотрим расчет 
на примере
|
№ К-во Просмотров: 381
Бесплатно скачать Контрольная работа: Статистическое изучение взаимосвязей
|