Контрольная работа: Свойства портландцемента. Основные свойства строительных материалов

Истинная плотность большинства строительных материалов больше единицы (за единицу условно принимают плотность воды при t = 4 °С). Для каменных материалов плотность колеблется в пределах 2200 – 3300 кг/м³ ; органических материалов (дерево, битумы, пластмассы) – 900 – 1600, черных металлов (чугун, сталь) – 7250 – 7850 кг/м³ .

Средняя плотность (r _ср ) – масса единицы объема материала (изделия) в естественном состоянии с пустотами и порами

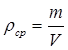, (2)

где – средняя плотность, кг/м³ ; т – масса материала (изделия) в естественном состоянии, кг; V – объем материала (изделия), м³ .

Если образец имеет правильную геометрическую форму, его объем определяют путем вычислений по измеренным геометрическим размерам; если же образец неправильной формы, – по объему вытесненной жидкости.

Для сыпучих материалов (песок, цемент, щебень, гравий) определяют насыпную плотность.

Насыпная плотность (r _н ) – масса единицы объема сыпучих материалов в свободном (без уплотнения) насыпном состоянии. Формула расчета и размерность показателя те же, что в (1) и (2). В единицу объема таких материалов входят не только зерна самого материала, но и пустоты между ними. Количество пустот, образующихся между зернами рыхлонасыпного материала, выраженное в процентах по отношению ко всему занимаемому объему, называют пустотностью.

Средняя плотность природных и искусственных материалов колеблется в широких пределах – от 10 кг/м³ (полимерный воздухонаполненный материал «мипора») до 2500 кг/м³ у тяжелого бетона и 7850 кг/м³ у стали.

Данные средней плотности используют при подборе материала для изготовления строительных конструкций, расчетах транспортных средств, подъемно-транспортного оборудования. При одинаковом вещественном составе средняя плотность характеризует прочностные свойства. Чем выше средняя плотность, тем прочнее материал.

Для пористых строительных материалов истинная плотность больше средней плотности. Только для абсолютно плотных материалов (металлы, стекла, лаки, краски) показатели средней и истинной плотности численно равны.

Важной характеристикой строительных материалов является их общая пористость (П) .

Поры бывают открытыми и условно закрытыми или замкнутыми. При этом

П_п =П₁ +П₂ ,

где П₁ , П₂ – доля, соответственно, открытых(капиллярных) и закрытых пор.

По величине истинной и средней плотности рассчитывают общую пористость (П_п ) материала в % (ГОСТ 12730.1-78)

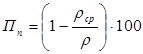(3)

Поры в материале могут иметь различную форму и размеры. Они могут быть открытыми, сообщающимися с окружающей средой, и замкнутыми, заполненными воздухом. При погружении материала (изделия) в воду открытые поры полностью или частично, что зависит от размера пор, заполняются водой. В замкнутые поры вода проникнуть не может.

Открытую или капиллярную пористость (W_о ) определяют, как и влажность по объему , по водонасыщению материала под вакуумом или кипячением его в воде

, (4)

где т – масса образца в сухом состоянии, г; m₁ – масса образца в водонасыщенном состоянии, г; V – объем образца, см³ .

Общая пористость различных по назначению материалов изменяется в широком диапазоне. Так, для тяжелого, прочного конструкционного бетона – 5 – 10 % , кирпича, который как стеновой материал должен обеспечить прочность, легкость стеновой конструкции и пониженную теплопроводность, – 25 – 35 % , для эффективного теплоизоляционного материала пенопласта – 95 %.

Большое влияние на свойства материалов оказывают не только величина пористости, но и размер пор, их характер (например, ячеистые поры – 0,2-10 ^–4 см; капиллярные – 10 ^–4 – 10 ^–5 см; гелевые поры – 10 ^-6 см).

При увеличении объема замкнутых пор и уменьшении их величины повышается морозостойкость материала и снижается теплопроводность. Наличие открытых крупных пор делает материал проницаемым для воды, неморозостойким, но в то же время он приобретает акустические свойства.

Влажность по массе материала определяется из выражения:

,

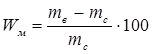где: m_в – масса образца в увлажненном состоянии,

m_с – масса образца, высушенного до постоянной массы.

Влажность материала по объему при его средней плотности ρ определяется из выражения:

Wo = ρ ^. Wm