Контрольная работа: Технология и производственная функция
Для производственной функции Кобба-Дугласа (В ) MRTSLK = ∆K/∆L и характеризуется убывающей по мере движения вдоль изокванты степенью замещения.
Для производственной функции с постоянной эластичностью замещения – CES – функции (Г ) MRTSLK = - b.
![]()
![]() K K
K K
 |
 |
![]()

![]()
![]() L L
L L
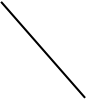
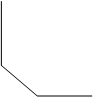
А) для функции Q = aK + bL Б) для функции Q = min(L/C1 ; К/C2 )
 K
K ![]()
![]() K
K
 |
 |
![]()
![]() L L
L L
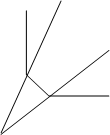
В) для функции Q = AKA LB Г) для функции
Q = e0 (e1 L –B + e2 K-B )* h/B
Рис.4 типы производственных функций.
Таким образом, подводя итог вышесказанному кратко сформулируем основные выводы:
1. Теория производства изучает соотношение между количеством применяемых ресурсов и объемом выпуска.
2. Основным инструментом анализа производства является производственная функция, которая описывает количественную зависимость между выпуском продукции и затратами ресурсов. Один и тот же объем выпуска может быть достигнут при различных комбинациях ресурсов (технологиях).
3. Линия на графике, показывающая разные сочетания производственных ресурсов и данный объем выпуска, называется изоквантой . Эти сочетания ресурсов (технологии) являются наиболее эффективными, т.к. любая точка на изокванте соответствует минимальным объемам ресурсов, необходимых для получения заданного объема готовой продукции. Изокванта обычно выпукла к началу координат вследствие предполагающейся взаимозаменяемости ресурсов. Когда ресурсы являются взаимодополняемыми, изокванта имеет L-образную форму. Когда ресурсы представляют собой совершенные субституты, прямая принимает форму прямой линии. Совокупность изоквант, отражающая максимально достижимый выпуск продукции при любом заданном наборе факторов производства называется картой изоквант.
В нижеприведенной таблице представлены данные об издержках, доходе, и спросе монополиста.
|
Q |
VC |
TC |
ATC |
MC |
P |
TR |
MR |
ПРИБЫЛЬ (УБЫТКИ) |
|
0 |
0 |
10 |
К-во Просмотров: 393
Бесплатно скачать Контрольная работа: Технология и производственная функция
|