Контрольная работа: Термодинамический расчет газового цикла
Таблица 1
Параметры состояния идеального газа в характерных точках цикла
|
Характерная точка |
|
|
| Примечание |
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 |
3.3. Определение массовых изобарной и изохорной теплоёмкостей.
Массовые изобарная и изохорная теплоёмкости (кДж/(кг·К)) определяется по формуле:
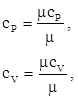
где ![]() – мольные изобарная и изохорная теплоёмкости, кДж/(кмоль ·К).
– мольные изобарная и изохорная теплоёмкости, кДж/(кмоль ·К).
Таблица 2
Приближенные значения мольных теплоемкостей при постоянном объеме и постоянном давлении (![]() ) [
) [![]() ]
]
| Газы | ||
| Одноатомные | 12,56 | 20,93 |
| Двухатомные | 20,93 | 29,31 |
| Трехатомные | 29,31 | 37,68 |
3.4. Процессы газового цикла.
Рассматриваемые процессы газа равновесные, т. е. состоят из равновесных промежуточных состояний, которые характеризуются одинаковым давлением, удельным объемом и температурой. Расчет процессов газового цикла начинается с процесса (1-2).
Уравнение первого закона термодинамики дает возможность исследовать явления, происходящие с газами при изменении его состояния.
В общем виде первый закон термодинамики представляет собой математическое выражение закона сохранения и превращения энергии. Его можно представить в таком виде ![]() :
:
![]() ,
,
т.е. подведенное к газу тепло расходуется на изменение внутренней энергии газа и на совершение работы.
Изменение энтальпии для термодинамических процессов ![]() определяется по формуле
определяется по формуле
![]()
Превращение работы в теплоту происходит всегда полностью, обратный же процесс превращения теплоты в работу при непрерывном переходе возможен лишь при определенных условиях. Второй закон термодинамики устанавливает условия преобразования тепловой энергии в механическую, определяет направление, в котором протекают процессы, а также максимальное значение работы, которая может быть произведена тепловым двигателем.
Для изучения процессов превращения тепла в работу в тепловых двигателях используют параметр состояния газа – энтропию газа.
В данной работе рассматривается прямой обратимый цикл. Второй закон термодинамики для обратимого процесса имеет вид ![]() :
:
![]()
Для вычисления изменения энтропии для термодинамических процессов (кроме адиабатного) используют логарифмические зависимости. В адиабатном процессе изменения состояния газа, в котором ![]() , энтропия не изменяется.
, энтропия не изменяется.
Если в прямом цикле в процессе расширения к газу подводится тепло в количестве ![]() , а в процессе сжатия от газа тепло отводится в количестве
, а в процессе сжатия от газа тепло отводится в количестве ![]() , то разность
, то разность ![]() как теплота исчезает в течение цикла в результате преобразования её в механическую энергию. Так как газ возвращается в первоначальное состояние, изменение внутренней энергии нет
как теплота исчезает в течение цикла в результате преобразования её в механическую энергию. Так как газ возвращается в первоначальное состояние, изменение внутренней энергии нет ![]() , т.е. в соответствии с первым законом термодинамики:
, т.е. в соответствии с первым законом термодинамики:
![]() ,
,