Контрольная работа: Уравнения регрессии
Далее находим F-критерий Фишера
![]() .
.
Для первого уравнения Fфакт.=18,906>Fтабл.=3,44, что подтверждает статистическую значимость уравнения. Для второго уравнения Fфакт.=30,360>Fтабл.=4,28, что подтверждает статистическую значимость уравнения. Для третьего уравнения Fфакт.=6,472>Fтабл.=4,28, что подтверждает его статистическую значимость. Итак, F-критерий Фишера подтверждает значимость всех трех уравнений с вероятностью 95%.
Для оценки значимости коэффициентов регрессии первого уравнения вычисляем t-критерий Стьюдента
![]() ,
,
где частный F-критерий
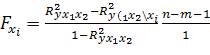 .
.
Получаем ![]() ,
, ![]() . Отсюда
. Отсюда ![]() ,
, ![]() . Для α=0,05
. Для α=0,05 ![]() . Следовательно, коэффициент регрессии b₁ является статистически значимым, а коэффициент b₂ таковым не является.
. Следовательно, коэффициент регрессии b₁ является статистически значимым, а коэффициент b₂ таковым не является.
Показатели частной корелляции для первого уравнения вычисляются по формуле
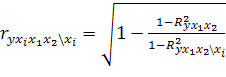 .
.
Получаем ![]() ,
, ![]() .
.
Средние коэффициенты эластичности для линейной регрессии рассчитываются по формуле
![]() .
.
Для первого уравнения получаем ![]() ,
, ![]() , для второго уравнения
, для второго уравнения ![]() , для третьего уравнения
, для третьего уравнения ![]() .
.
Задание 3
Исходная система уравнений
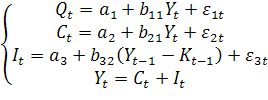
содержит эндогенные четыре переменные ![]() и две предопределенные
и две предопределенные ![]() .
.
В соответствии с необходимым условием идентификации D+1=H первое и второе уравнения сверхидентифицируемы (H=2, D=2), третье уравнение идентифицируемо (H=1, D=0), четвертое уравнение является тождеством и в проверке не нуждается.
Для первого уравнения
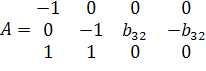 , Det A*≠0, rk A=3.
, Det A*≠0, rk A=3.
Для второго уравнения
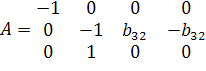 , Det A*≠0, rk A=3.
, Det A*≠0, rk A=3.
Для третьего уравнения
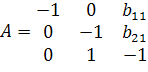 , Det A*≠0, rk A=3.
, Det A*≠0, rk A=3.
Четвертое уравнение является тождеством и в проверке не нуждается.
Достаточное условие идентификации выполняется для всех уравнений.
Для оценки параметров данной модели применяется двухшаговый МНК.
Приведенная форма модели