Контрольная работа: Вариационные ряды

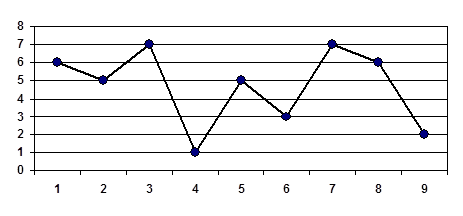
г) вычисление среднего значения СВ, дисперсии, среднеквадратичного отклонения:

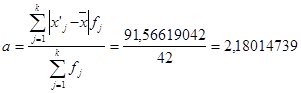
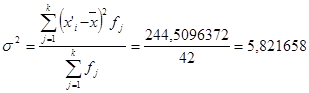
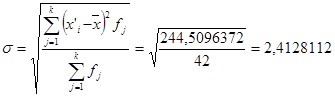
Задание № 2.

По заданной выборке проверить гипотезу о нормальном распределении СВ по критерию согласия Пирсона. Произвести интервальную оценку выборочного среднего значения с доверительной вероятностью 0,98

Таблица 1.

78	80	83	84	84	86	88	88	89	89	91	91	92	92	94	94	96	96	96	97	97	99	99	101	102
102	104	104	105	105	107	109	110	110	115	120	76	78	81	83	84	86	86	88	88	89	89	91	92	92
92	94	94	96	96	97	97	99	99	99	101	102	104	104	105	105	107	107	110	110	112	115	75	78	80
83	84	86	86	88	88	89	91	91	91	92	92	94	94	96	96	97	97	99	99	101	101	102	102	104
104	105	107	109	109	112	115	117	73	81	84	84	86	88	89	91	91	92	94	96	96	97	99	101	101
104	105	105	107	107	110	117	123	67	78	81	81	83	84	84	86	86	88	88	88	89	89	91	91	91
92	92	92	94	94	94	96	96	97	97	97	99	99	99	101	101	102	102	104	104	104	105	105	107	107
109	109	110	110	113	118	121

№=182

Решение.

Вычислим число групп в вариационном ряду пользуясь формулой Стерджесса:

Определим величины интервала:

Примем число групп равным 8, а число интервалов 7.

Таблица 2.

Номер интервала	xj	fj	x’j	x’j fj	f’j
1	2	3	4	5	6
1	67-74 (+)	2	70,5	141	2
2	74-81	12	77,5	930	14
3	81-88	30	84,5	2535	44
4	88-95	40	91,5	3660	84
5	95-102	47	98,5	4629,5	131
6	102-109	32	105,5	3376	163
7	109-116	13	112,5	1462,5	176
8	116-123	6	119,5	717	182
Итого	182	17451

Условные обозначения в таблице: x_j - установленные интервалы; f_j - частота событий; x’_j - середина интервала; f’_j - накопленная частота.

На основании полученных данных построим таблицу 2.

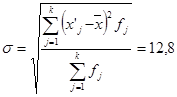
Значения и находим по таблице значений функции Лапласа.

P_j определяется разностью и , а f’_j = P_j * n.

Таблица 3.

Номер интервала	Границы интервала		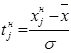		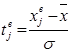	Pj	f’j
1	2	3	4	5	6	7	8
1	67-74	-2,26	-1,70	-0,4881	-0,4554	0,0327	5,9514
2	74-81	-1,70	-1,16	-0,4554	-0,3770	0,0784	14,2688
3	81-88	-1,16	-0,61	-0,3770	-0,2291	0,1479	26,9178
4	88-95	-0,61	-0,06	-0,2291	-0,0279	0, 2012	38,0268
5	95-102	-0,07	0,47	-0,0279	0,1808	0, 2087	37,9834
6	102-109	0,47	1,02	0,1808	0,3461	0,1653	30,0846
7	109-116	1,02	1,57	0,3461	0,4418	0,0957	17,4174
8	116-123	1,57	2,12	0,4418	0,4830	0,0412	7,4984
Итого

Условные обозначения в таблице:

x^н _j - нижняя граница интервала;

x^в _j - верхняя граница интервала;

t^н _j и t^в _j - нормированные отклонения для нижней и верхней границ интервала;

и - значение интегральной функции Лапласа для t^н _j и t^в _j ;

P_j - оценка вероятности попадания в интервал;