Контрольная работа: Вариационные ряды
Итак, воспользуемся данными таблицы 1 и 2 для расчета критерия "хи-квадрат", предварительно округлив теоретические частоты в графе 8 табл.2, а также объединив частоты двух последних интервалов, выполняя требование f’j ³ 5.
Таблица 4.
| Номер интервала | Эмпирические частоты | Теоретические частоты |  |  |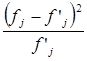
| 1 | 2 | 6 | 16 | 2,67 |
| 2 | 12 | 14 | 4 | 0,29 |
| 3 | 30 | 27 | 9 | 0,33 |
| 4 | 40 | 38 | 4 | 0,1 |
| 5 | 47 | 38 | 81 | 2,13 |
| 6 | 32 | 30 | 4 | 0,13 |
| 7 | 16 | 25 | 81 | 3,24 |
| Итого | 182 | 178 | 8,89 |
X2 расч = 8,89
Таким образом, проведенный расчет дает право не отвергать гипотезу о нормальном характере эмпирического распределения.
Произведем интервальную оценку выборочного среднего значения с доверительной вероятностью 0,98.
На основе имеющейся выборки получим точечную оценку математического ожидания в виде выборочной средней:
Среднеквадратичное отклонение составляет: 
. Уровень надежности 
. Определяем значение функции Лапласса:
По таблице значений функции 
находим соответствующее значение z . В данном случае 
. Тогда 
.
Доверительный интервал] 95,6868 - 0,164, 95,6868 + 0,164 [=
=] 95,5228, 95,8508 [.
Следовательно, 95,5228 < Mx < 95,8508 с вероятностью 0,98.
Задание № 4.
По заданной выборке (x,y) найти коэффициент корреляции и уравнения линейной регрессии y=a+b*x, №=45
Таблица 5
| x…... y | x…... y | x…... y | x…... y | x…... y | x…... y | x…... y | x…... y | x…... y | x…... y | x…... y | |||||||||||
| 23 | -115 | 18 | -90 | 10 | -48 | 19 | -91 | 18 | -84 | 9 | -44 | 12 | -55 | 24 | -115 | 6 | -26 | 22 | -107 | 18 | -84 |
| 18 | -83 | 11 | -54 | 15 | -71 | 13 | -64 | 8 | -51 | 14 | -64 | 22 | -109 | 8 | -38 | 14 | -64 | 22 | -106 | 9 | -43 |
| 16 | -74 | 17 | -85 | 15 | -71 | 13 | -60 | 11 | -37 | 24 | -118 | 18 | -87 | 6 | -28 | 7 | -31 | 22 | -109 | 13 | -64 |
| 8 | -35 | 8 | -35 | 12 | -56 | 12 | -54 | 14 | -67 | 14 | -68 | 21 | -102 | 10 | -46 | 16 | -79 | 17 | -80 | 18 | -87 |
| 22 | -105 | ||||||||||||||||||||
Решение:
На основании исходных данных найдем суммы и средние значения x и y :
Вычислим параметр парной линейной корреляции:
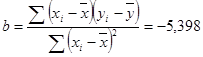
Свободный член уравнение регрессии вычислим по формуле:
, откуда 
Уравнение регрессии в целом имеет вид:
Коэффициент корреляции, рассчитанный на основе полученных данных:
