Контрольная работа: Визначення площі між функціями інтегралом за методом трапеції на мові Pascal

Зміст

1. Постановка задачі3

2. Математичний опис рішення задачі4

3. Алгоритм програми. 6

4. Лістинг програми. 7

5. Контрольний приклад. 10

Список використаної літератури. 11

Постановка задачі

Скласти програму на мові Pascal розрахунку за методом трапецій площі між графіками функцій F1(x) = cos x² + 1 i F2(x) = 2^{x^2} з точністю е = 0,0001.

2. Математичний опис рішення задачі

Розрахунок за методом трапецій площі між графіками функцій F1(x) = cos x² + 1 i F2(x) = 2^{x^2} (рис.1) здійснюється вирішенням визначеного інтегралу 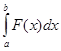, який саме і визначає площі під графіками. За властивістю інтегралів 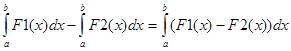, тому в якості підінтегральної функції ми беремо функцію F(x) = cos x² + 1 - 2^{x^2}

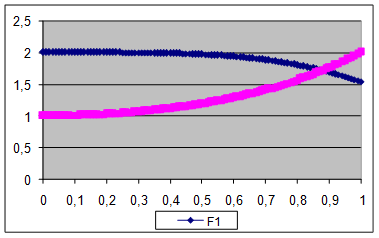
Рис.1.

Саме метод трапеції реалізований на мові Pascal у наступному фрагменту програми, у якому для розрахунків використано цикл із заздалегідь визначеним числом повторень:

h:=(b-a)/n;

yp:=0;

x:=a;

for i:=1 to n-1 do

begin

x:=x+h;

yp:=yp+(cos(sqr(x))+1-exp(sqr(x)*ln(2)));

end;

yn:=cos(sqr(a))+1-exp(sqr(a)*ln(2));

yk:=cos(sqr(b))+1-exp(sqr(b)*ln(2));

s:=((yk+yn)/2+yp)*h;

де,

n – кількість відрізків, на які розбивається дільниця інтегрування;

i – допоміжна змінна циклу;

a – початкова межа інтегрування;

--> ЧИТАТЬ ПОЛНОСТЬЮ <--