Контрольная работа: Водорастворимые полимеры

При конечной концентрации полимера и при добавлении соли происходит экранирование. Если, то расстояние между концами полимерной цепи описывается следующим скейлинговым выражением:

Это выражение выполняется, если для полимерной цепи характерно отталкивание на коротких расстояниях. Для макромолекулярной цепи, в которой действует притяжение, предельным случаем является плотная глобула, и расстояние между концами цепи равно

Для незаряженных полимеров можно изменять величину R_tt путем замены растворителя. Хороший растворитель соответствует эффективному отталкиванию между мономерными звеньями. Плохой растворитель вызывает сжатие макромолекулы из-за эффективных взаимодействий притяжения. На величину R_tt полиэлектролитов можно влиять различными способами. Например, увеличение концентрации полимера в растворе увеличивает экранирование взаимодействий и приводит к уменьшению R_tt . То же самое наблюдается и при введении в раствор соли. Другой способ - варьирование рН, что приводит либо к нейтрализации зарядов, либо к ионизации функциональных групп мономеров. Расстояние между концами цепи в этом случае увеличивается пропорционально степени ионизации б. Для слабо заряженного полиэлектролита даже в присутствии соли расстояние между концами цепи зависит от б следующим образом:

4. Простейшая скейлинговая теория

В этом разделе выведены некоторые приведенные выше соотношения для расстояния между концами полиэлектролитных цепей. Это можно сделать простым способом, рассматривая, как различные вклады в свободную энергию зависят от конфигурации цепи. Такой подход имеет ряд ограничений, но позволяет оценить некоторые важные физические свойства. Построим полиэлектролитную цепь как набор зарядов, связанных жесткими связями.

При расчете энергии электростатического взаимодействия будем считать, что заряды расположены на прямой линии длиной R = га, где а - средняя длина связи мономер-мономер. Далее суммируя все парные взаимодействия в цепи, состоящей из г мономеров, получим выражение для энергии электростатического взаимодействия:

где /в) известно как бьеррумовская длина, а пренебрежимо малый постоянный член опущен. Энтропия вытягивания цепи принимается равной энтропии идеальной цепи:

Опуская тривиальные константы, запишем выражение свободной энергии для всей цепи:

Оптимизируя уравнение, полагая R = R_ee и пренебрегая вариацией логарифмического члена, найдем оптимальную свободную энергию из условия

Рис. Схематическая модель полиэлектролита

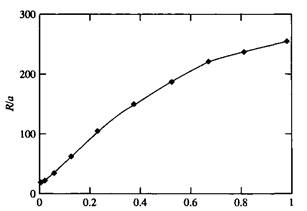
Рис. Степень ионизации б

Зависимость усредненного расстояния между концами полимерной цепи R_ee от степени ионизации б по данным моделирования методом Монте-Карло. R_ee нормировано на величину а, г = 320 откуда находим, что R_qq изменяется по закону

Найденное выражение справедливо для полиэлектролитной цепи при бесконечном разбавлении и в отсутствие солей.

Уравнение справедливо и для слабых полиэлектролитов. Полиэлектролит в этом случае состоит из титруемой цепи, заряд которой изменяется с рН. Считая, что каждое мономерное звено несет локальный заряд, равный степени диссоциации а, энергию электростатического взаимодействия можно записать в виде

Используя ту же процедуру, найдем, что расстояние между концами полиэлектролитной цепи зависит от б в степени 2/3:

5. Простейшая скейлинговая теория для систем в присутствии солей

В реальных системах всегда присутствуют соли, которые влияют на электростатические взаимодействия, так как экранируют заряженные мономерные звенья. Взаимодействие экранируется и другими цепями, и противоионами, снижающими радиус действия электростатического взаимодействия. В первом приближении для описания взаимодействия между двумя мономерами на расстоянии г друг от друга можно использовать выражение Дебая-Хюккеля:

Взаимодействия в этом случае короткодействующие, и, по-видимому, для нахождения электростатической энергии нельзя моделировать систему прямой линией с расположенными на ней зарядами. Вместо этого принимают, что цепь усредненно можно считать сферой радиусом R. Потенциал Дебая-Хюккеля имеет громоздкий вид и его трудно использовать для оценок, но его можно упростить, полагая, что взаимодействие мономерных звеньев строго соответствует кулоновскому потенциалу, но только на расстояниях, не превышающих к~ *. Используя, как и ранее, энтропию идеальной цепи, получим следующее выражение для свободной энергии: