Контрольная работа: Задачи линейного программирования. Алгоритм Флойда

Перейдем теперь к рассмотрению более общих моделей и задач.

Простейшая задача производственного планирования. Пусть имеется некоторый экономический объект (предприятие, цех, артель и т. п.), который может производить некоторую продукцию п видов. В процессе производства допустимо использование т видов ресурсов (сырья). Применяемые технологии характеризуются нормами затрат единицы сырья на единицу производимого продукта. Обозначим через a_{i , j} количество i-го ресурса (iÎ1: m), которое тратится на производство единицы j-го продукта (jÎ1:n). Весь набор технологических затрат в производстве j-го продукта можно представить в виде вектора-столбца

а технологию рассматриваемого предприятия (объекта) в виде прямоугольной матрицы размерности т на п:

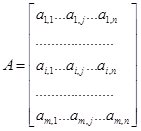
Если j-й продукт производится в количестве x_j , то в рамках описанных выше технологий мы должны потратить a_{1, j} x_j первого ресурса, a_{2, j} x_j — второго, и так далее, a_mj x_j — т-го. Сводный план производства по всем продуктам может быть представлен в виде n-мерного вектора-строки x = (x_1, x₂ ,...,x_j ,...,x_n ) . Тогда общие затраты по i-му ресурсу на производство всех продуктов можно выразить в виде суммы

представляющей собой скалярное произведение векторов а_j и х. Очевидно, что всякая реальная производственная система имеет ограничения на ресурсы, которые она тратит в процессе производства. В рамках излагаемой модели эти ограничения порождаются m-мерным вектором b = (b_1, b₂ ,...,b_m ), где b_i — максимальное количество i-го ресурса, которое можно потратить в производственном процессе. В математической форме данные ограничения представляются в виде системы т неравенств:

a_1,1 x_l +a_l,2 x₂ +...+a_l,n x_n £ b_l ,

o_2,l x_l +a_2,2 x₂ +...+a_2,n x_n £ b₂ ,

a_m ,_l x_l +a_m,2 x₂ +...+a_m,n x_n £ b_n .(7)

Применяя правила матричной алгебры, систему (7) можно записать в краткой форме, представив левую часть как произведение матрицы А на вектор х, а правую — как вектор b:

Ах £ b. (8)

К системе (8) также должны быть добавлены естественные ограничения на неотрицательность компонентов плана производства: x₁ , ³ 0,..., x_j ³0, ..., х_п ³0, или, что то же самое,

x³ 0. (9)

Обозначив через с_j цену единицы j-го продукта, получим выражение суммарного дохода от выполнения плана производства, задаваемого вектором х:

(10)

Формулы (8)-(10) являются не чем иным, как простейшей математической моделью, описывающей отдельные стороны функционирования некоторого экономического объекта, поведением которого мы хотим управлять. В рамках данной модели, вообще говоря, можно поставить различные задачи, но, скорее всего, самой «естественной» будет задача поиска такого плана производства xÎRⁿ , который дает наибольшее значение суммарного дохода, т. е. функции (10), и одновременно удовлетворяет системе ограничений (8)-(9). Кратко такую задачу можно записать в следующем виде:

где (11)

Несмотря на явную условность рассматриваемой ситуации и кажущуюся простоту задачи (11), ее решение является далеко не тривиальным и во многом стало практически возможным только после разработки специального математического аппарата. Существенным достоинством используемых здесь методов решения является их универсальность, поскольку к модели (11) могут быть сведены очень многие как экономические, так и неэкономические проблемы.

Поскольку любая научная модель содержит упрощающие предпосылки, для корректного применения полученных с ее помощью результатов необходимо четкое понимание сути этих упрощений, что, в конечном счете, и позволяет сделать вывод об их допустимости или недопустимости. Наиболее «сильным» упрощением в рассмотренной модели является предположение о прямо пропорциональной (линейной) зависимости между объемами расхода ресурсов и объемами производства, которая задается с помощью норм затрат а_{i , j} . Очевидно, что это допущение далеко не всегда выполняется. Так, объемы расхода многих ресурсов (например, основных фондов) изменяются скачкообразно в зависимости от изменения компонентов объема производства х. К другим упрощающим предпосылкам относятся предположения о независимости цен с_j от объемов х_j , что справедливо лишь для определенных пределов их изменения, пренебрежение эффектом кооперации в технологиях и т. п. Данные «уязвимые» места важно знать еще и потому, что они указывают принципиальные направления совершенствования модели.

2 Алгоритм Флой д а. Постановка задачи

Этот алгоритм более общий по сравнению с алгоритмом Дейкстры, так как он находит кратчайшие пути между любыми двумя узлами сети. В этом алгоритме сеть представлена в виде квадратной матрицы с n строками и n столбцами. Элемент (i, j) равен расстоянию dij от узла i к узлу j, которое имеет конечное значение, если существует дуга (i, j), и равен бесконечности в противном случае.

Основная идея метода Флойда. Пусть есть три узла i, j и k и заданы расстояния между ними (рис. 1). Если выполняется неравенство dij + djk < dik, то целесообразно заменить путь i -> k путем i -> j -> k. Такая замена (далее ее будем условно называть треугольным оператором) выполняется систематически в процессе выполнения алгоритма Флойда.

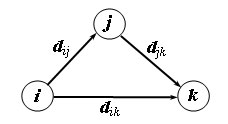
Рис.1. Треугольный оператор

Определяем начальную матрицу расстояния D0 и матрицу последовательности узлов S0. Диагональные элементы обеих матриц помечаются знаком "-", показывающим, что эти элементы в вычислениях не участвуют. Полагаем k = 1:

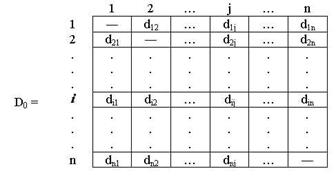
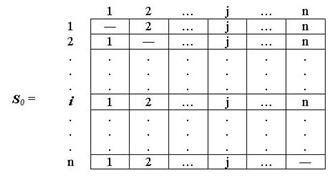
Рис.2. Начальная ситуация

Основной шаг k. Задаем строку k и столбец k как ведущую строку и ведущий столбец. Рассматриваем возможность применения треугольного оператора ко всем элементам dij матрицы Dk-1. Если выполняется неравенство dik + dkj < dij, (i <> k, j <> k, i <> j), тогда выполняем следующие действия:

создаем матрицу Dk путем замены в матрице Dk-1 элемента dij на сумму dik + dkj,

создаем матрицу Sk путем замены в матрице Sk-1 элемента sij на k. Полагаем k = k + 1 и повторяем шаг k.

Поясним действия, выполняемые на k-м шаге алгоритма, представив матрицу Dk-1 так, как она показана на рисунке 3. На этом рисунке строка k и столбец k являются ведущими. Строка i - любая строка с номером от 1 до k - 1, а строка p - произвольная строка с номером от k + 1 до n. Аналогично столбец j представляет любой столбец с номером от 1 до k - 1, столбец q - произвольный столбец с номером от k + 1 до n. Треугольный оператор выполняется следующим образом. Если сумма элементов ведущих строки и столбца (показанных в квадратах) меньше элементов, находящихся в пересечении столбца и строки (показанных в кружках), соответствующих рассматриваемым ведущим элементам, то расстояние (элемент в кружке) заменяется на сумму расстояний, представленных ведущими элементами:

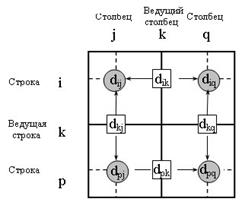
Рис.3. Иллюстрация алгоритма Флойда

После реализации n шагов алгоритма определение по матрицам Dn и Sn кратчайшего пути между узлами i и j выполняется по следующим правилам.