Контрольная работа: Завдання лінійного програмування

2. Графічний метод рішення

Двовимірні завдання лінійного програмування звичайно вирішуються графічно.

Алгоритм рішення задачи двумірного лінійного програмування графічним методом:

1. Будуємо область припустимих рішень функції F.

Для цьго в обмеженнях змінюємо знак нерівності на знаки рівняння і будуємо прямі. Далі визначаємо ті полуплощини, які відповідають обмеженням та отримуємо область припустимих значень, яка знаходиться на перетинанні всіх полуплощин.

2. Будуємо пряму рівня.

Для цьго обираємо будь яку точку М, яка належить до області припустимих рішень функції F, та підставивиши координати цієї точки в функцію, отримуємо пряму рівня. Далі від обраної точки М відкладуємо вектор а, координаті якого – це коефіціенти при цільвій функції F.

3. Максимізуємо (мінімізуємо) цільову функцію F.

Для максимізації (мінімізації) цільової функції F пересуваємо пряму рівня у напрямку, (в протилежному напрямку відносно) вектора а до перетинання з граничною точкою області припустимих рішень. Отримана точка є оптимальним рішенням, в якому функція досягає свого максимуму (мінімуму). Знаходимо координати цієї точки та підставляємо їх в функцію F.

3. Приклад 1

Вирішимо отримане двовимірне завдання лінійного програмування графічно:

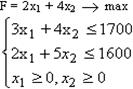
Рішення:

Побудова області припустимих рішень цільової функції F

Побудуємо прямокутну систему координат, де вісь ОX позначимо за x₁ , а OY - за x₂ .

Тому що, відповідно до умови (3) x₁ й x₂ ненегативні, то можна обмежиться розгляданням першого квадранта.

Розглянемо перше обмеження:

3x₁ +4x₂ <=1700 (1)

Замінимо в даному обмеженні знак нерівності знаком рівняння й побудуємо пряму.

3x₁ +4x₂ =1700 (1')

Для цього знайдемо дві крапки, що належать даній прямій.

Нехай, наприклад, x₁ =0, тоді підставивши 0 в (1') одержимо 4x₂ =1700 або x₂ =425.

(0: 425) - координати першої крапки, що належить прямій.

Нехай x₂ =0, те 3x₁ =1700, отже, x₁ =567.

(567:0) - координати другої крапки, що належить прямій.

Відзначимо ці крапки на числових осях.

Аналогічно, для другого обмеження:

2x₁ +5x₂ <=1600 (2)

2x₁ +5x₂ =1600 (2')