Курсовая работа: Алгоритмы обработки данных линейной и нелинейной структуры
Индекс его родителя равен (n-2)/2, и он определяет последний нелистовой узел пирамиды. Этот индекс является начальным для преобразования массива.
Рассмотрим целочисленный массив
int A[10] = {9, 12, 17, 30, 50, 20, 60, 65, 4, 19};
Индексы листьев: 5, 6, ..., 9.
Индексы родительских узлов: 4, 3, ..., 0.
Родитель А[4]=50, он больше своего сына А[9]=19 и поэтому должен поменяться с ним местами.
Родитель А[3]=30, он больше своего сына А[8]=4 и поэтому должен поменяться с ним местами (если меньших сына два, то меняется местами с наименьшим сыном).
На уровне 2 родитель А[2]=17 уже удовлетворяет условию пирамидальности, поэтому перестановок не производится.
Родитель А[1]=12 больше своего сына А[3]=4 и должен поменяться с ним местами.
Процесс прекращается в корневом узле. Родитель А[0]=9 должен поменяться местами со своим сыном А[1].
Результирующее дерево является пирамидой.
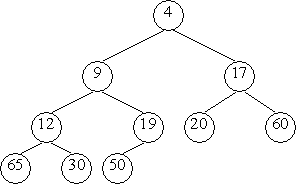
Включение элемента в пирамиду
1. Новый элемент добавляется в конец списка.
2. Если новый элемент имеет значение, меньшее, чем у его родителя, узлы меняются местами.
3. Новый родитель рассматривается как сын, и проверяется условие пирамидальности для более старшего родителя.
4. Процесс сканирует путь предков и завершается, встретив родителя, меньше чем новый элемент, или достигнув корневого узла.
Удаление из пирамиды
Данные удаляются всегда из корня дерева.
1. Удалить корневой узел и заменить его последним узлом.
2. Если новый корневой узел больше любого своего сына, то необходимо его поменять местами с наименьшим сыном.
3. Движение по пути меньших сыновей продолжается до тех пор, пока элемент не займет правильную позицию в качестве родителя или пока не будет достигнут конец списка.
2. Структурная схема программы с описанием
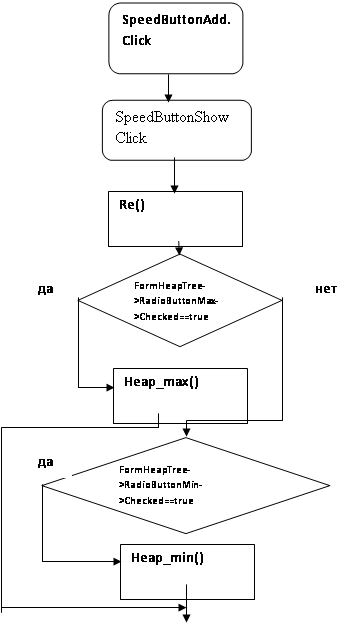
Схема взаимодействия функций программного комплекса:
 | ||
 | ||
 | ||
| ||

![]()

![]()

![]()
|
|
|
![]()
![]()
![]()

|

|
|
|
Структурные схемы алгоритмов:
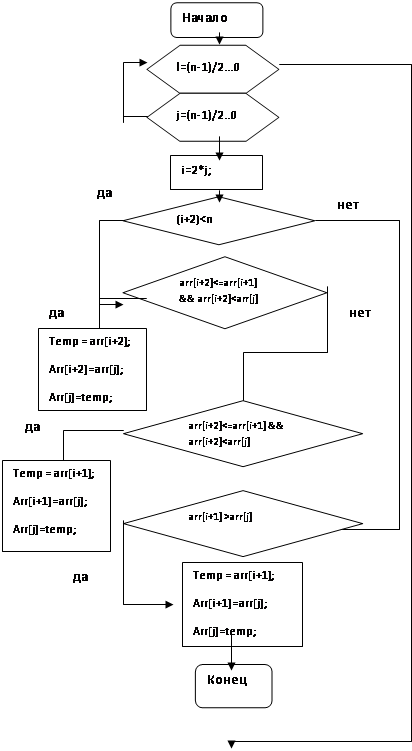
Преобразование массива в максимальную пирамиду
 | ||