Курсовая работа: Анализ и синтез электрических фильтров
,
- период,
,
- функции, составляющие ортогональный базис.
Разложение справедливо для периодических функций (
), заданных на всей числовой оси 
до 
.
Данную функцию нельзя разложить в тригонометрический ряд Фурье, так как она не периодическая. Доопределим данную функцию на всю числовую ось (рис. 2.1). В данном случае функция не является ни чётной, ни нечётной. Для такого сигнала справедливо общее разложение, содержащее постоянную составляющую, косинусы и синусы.
Кроме периодичности полученная функция удовлетворяет всем условиям теоремы Дирихле:
1. она непрерывна на отрезке 
и имеет конечное число точек разрыва первого рода;
2. она имеет конечное число экстремумов на этом отрезке.
Следовательно, к полученной функции можно применить разложение в тригонометрический ряд Фурье.
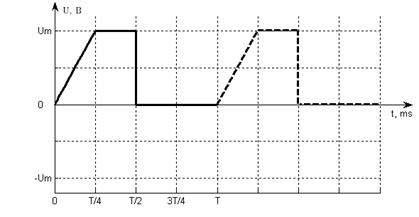
Рис. 2.1
Запишем аналитическое выражение для данной функции:
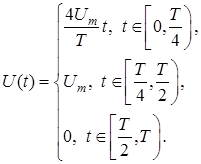
Вычислим с помощью пакетаMATLAB 6.5(7.0) и m - file : Fourier . m коэффициенты Фурье 
для двадцати гармоник.
Таблица 2 . 1
Результатов вычислений:
|
Коэффициенты Фурье для данной функции F(x), заданной графически на отрезке [0,T]. | |
Коэффициенты  | Коэффициенты  |
|
A(0)= 75.000 A(1)= -20.264 A(2)= -10.132 A(3)= -2.252 A(4)= -0.000 A(5)= -0.811 A(6)= -1.126 A(7)= -0.414 A(8)= -0.000 A(9)= -0.250 A(10)= -0.405 К-во Просмотров: 634
Бесплатно скачать Курсовая работа: Анализ и синтез электрических фильтров
| |