Курсовая работа: Анализ модели на чувствительность

Если условие оптимальности не выполняется, следует применить (прямой) симплекс-метод для получения нового оптимального решения.

Предположим, что фабрика игрушек TOYCO проводит новую ценовую политику относительно своих изделий. В соответствии с этим доход от одной модели поезда, грузовика и легкового автомобиля составляет соответственно , и . Получаем новую целевую функцию для этой модели

Максимизировать

.

Поскольку текущее базисное решение состоит из переменных х₂ , х₃ и х₆ , имеем . Вычислим вектор двойственных цен.

.

Разности для небазисных переменных , и вычисляются по формуле :

,

,

.

Отметим, что здесь использовалось новое значение коэффициента целевой функции .

Вычисления показывают, что текущее решение , и остается оптимальным. Новое значение целевой функции равно

.

Предположим, что в рассматриваемой задаче целевая функция имеет следующий вид.

Максимизировать .

Эта функция совпадает с предыдущей целевой функцией, за исключением того, что коэффициент при переменной теперь равен . Поэтому необходимо пересчитать только разность . В результате получаем следующее.

Отсюда следует, что переменную необходимо включить в базисное решение. Имеем следующую симплекс-таблицу.

Базис Решение

Новые значения разностей для небазисных переменных , и в симплекс-таблице выделены. Все остальные элементы таблицы остались такими же, как и в исходной таблице с оптимальным решением. Для нахождения нового оптимального решения следует ввести в базис переменную и исключить из него переменную . В результате получим решение , , и

Кроме того; для исследования влияния коэффициентов целевой функции на оптимальность решения можно также вычислить (по отдельности) интервалы изменения каждого коэффициента, сохраняющие оптимальность текущего решения. Для этого следует заменить текущий коэффициент су выражением , где — величина (положительная или отрицательная) изменения коэффициента .

Ограничения на величины можно определить путем вычисления новых разностей и наложения на них соответствующего условия оптимальности, которое зависит от того, рассматривается ли задача минимизации или максимизации.

Пусть в задаче о фабрике игрушек TOYCO нас интересует интервал допустимости для значения фонда рабочего времени первой операции. Заменим вектор вектором

.

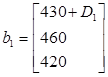Переменная представляет изменения фонда рабочего времени первой операции по сравнению с текущим уровнем в минут. Для того чтобы текущее базисное решение осталось недопустимым, необходимо выполнение неравенства . Отсюда получаем следующую систему неравенств.