Курсовая работа: Аппроксимация экспериментальных зависимостей

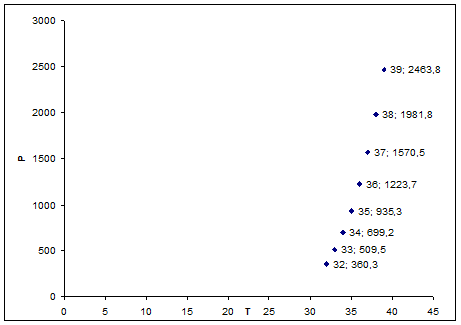
Рис. 1.Экспериментальная зависимость P=f(T)

В результате анализа данных выберем в качестве аппроксимирующего многочлена параболу, заданную уравнением P₂ (x)=a₀ +a₁ x+a₂ x² .

Для определения коэффициентов a₀ , a₁ , a₂ запишем систему уравнений вида

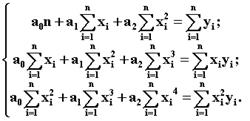
При составлении системы создадим вспомогательную таблицу данных (таблица 2).

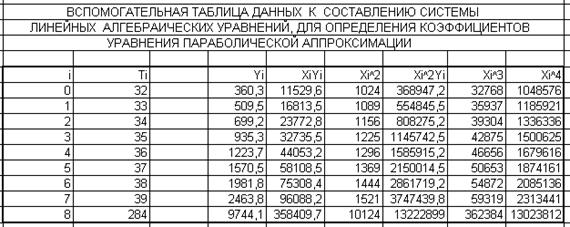
Используя данные таблицы 2, систему уравнений (5) записываем в виде

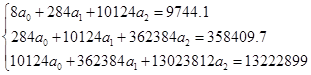
В результате решения системы методом Крамера получаем следующие значения определителей:

detA = 56448;

detA1 = 1435933397;

detA2 = -94279012,8;

detA3 = 1564382,4;

Вычислив определители, рассчитываем значения коэффициентов:

a₀ = detA1/ detA;

a₁ = detA2/detA;

a₂ = detA3/ detA;

a₀ = 25438,1625;

a₁ = -1670,19226;

a₂ = 27,71369048.

Таким образом, искомый аппроксимирующий многочлен имеет вид:

(6)

Полученная аналитическая зависимость (6) обобщает экспериментальные данные табл.01.

Для оценки погрешности полученной зависимости составим таблицу значений P. Для этого определим давление P по формуле (6). Результаты внесем в таблицу 2.

Таблица 2

T	32	33	34	35	36	37	38	39
P	370,8291668	502,0267858	688,6518	930,7042	1228,1839	1581,091	1989,4256	2453,188

Для оценки точности параболической аппроксимации сравниваем значения Р из табл.01 и табл.2. Модуль разности соответствующих значений представляет DP-погрешность аппроксимации, значения которой представлены в табл.3. В таблице приведена также относительная погрешность dР, равная отношению DР к Р.

Таблица 3

Т	32	33	34	35	36	37	38	39
DР	10,529	7,4732	0,5482	4,59583	4,4839	10,591	7,625	10,6125
dP,%	2,8393578	1,4886087	1,5317	0,4938	0,36509	0,6699	0,38331	0,4326

Сравнительный анализ погрешностей показывает, что полученная аналитическая зависимость удовлетворительно обобщает исходные экспериментальные данные.