Курсовая работа: Аппроксимация экспериментальных зависимостей

Задание 1

Данные давления водорода Н₂ на линии насыщения приведены в таблице. Сделать аппроксимацию экспериментальных данных в виде степенной функции и многочлена первой степени. Произвести сравнительный анализ ошибки аппроксимации полученной двумя функциями.

Таблица 1

Ts ,0 К	32	33	34	35	36	37	38	39
Pмм рт. ст.	360,3	509,5	699,2	935,3	1223.7	1570,5	1981,8	2463,8

Аппроксимация экспериментальных зависимостей методом наименьших квадратов. Теоретические сведения

Пусть, в результате эксперимента получена зависимость.

Необходимо найти аналитическую формулу f = , которая аппроксимирует экспериментальную (табличную) зависимость.

Выберем зависимость в виде полинома 2 – й степени, т.е.

(1)

В выражении (1) коэффициенты , , подлежат определению, причем эти коэффициенты должны быть подобраны таким образом, чтобы зависимость наилучшим образом приближалась к экспериментальной зависимости. Пусть отклонение - различие между табличным значением в точке и значением аналитической функции в этой же самой точке, т.е.:

(2)

В соответствии с методом наименьших квадратов (МНК) наилучшими коэффициентами зависимости (1) будут такие, для которых сумма квадратов отклонений будет минимальной.

(3)

Используя необходимые условия существования экстремума для функций нескольких переменных , находим уравнение для определения коэффициентов зависимости (1).

(4)

Из условия (4) получим систему линейных алгебраических уравнений:

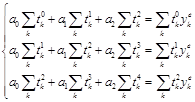(5)

Решив систему (5) найдем коэффициенты аппроксимирующей зависимости (1).

Эффективным методом решения систем линейных алгебраических уравнений является матричный метод. Сущность его состоит в следующем.

Пусть А — матрица коэффициентов системы уравнений, X — вектор неизвестных, В — вектор правых частей системы уравнений. Тогда решение системы уравнений в матричной форме будет иметь вид:

Х = А ^-1 В.

Правило Крамера

Если ранг матрицы совместной системы равен числу ее неизвестных, то система является определенной. Если число неизвестных системы совпадает с числом уравнений ( m = n ) и матрица системы невырожденная (detA ≠ 0), то система имеет единственное решение, которое находится по правилу Крамера:

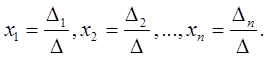
В этих формулах ∆ = detА — определитель системы, а ∆_k — определитель, полученный из определителя системы заменой k -г o столбца столбцом свободных членов ( k = 1, 2,..., n ).

Решение системы трех линейных уравнений с тремя неизвестными можно выразить через определители:

, ,

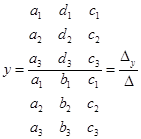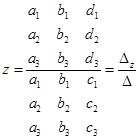
Информационное обеспечение

Зависимость давления P водорода Н₂ при различных температурах на линии насыщения приведены в таблице (1).

Для проведения анализа исходных данных с целью выбора вида аппроксимирующего многочлена построим график функции, заданной в табл.1. График приведен на рис.1.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--