Курсовая работа: Автоматический потенциометр с кулачковым механизмом

Истинные значения хода толкателя и аналога скорости получают умножением соответствующих ординат графиков на их масштабы (табл.1)

Таблица 1

, мм чер	мм	в μs	S, мм чер	S, мм
1	12	7,644	11,46	2	1,334
2	25	15,925	23,88	7	4,669
3	37	23,569	35,336	15	10,005
4	5	31,85	47,75	26	17,342
5	32	20,384	30,56	36	24,012
6	16	10,192	15,28	42	28,014
7	0	0	0	45	30,015
8	0	0	0	45	30,015
9	0	0	0	45	30,015
10	0	0	0	45	30,015
11	0	0	0	45	30,015
12	0	0	0	45	30,015
13	0	0	0	45	30,015
14	11	7,007	10,51	43	28,681
15	22	14,014	21,01	39	26,013
16	34	21,658	32,47	32	21,344
17	44	28,028	42,02	23	15,341
18	34	21,658	32,47	13	8,672
19	22	14,014	21,01	6	4,002
20	11	7,007	10,51	2	1,334
21	0	0	0	0	0
2	0	0	0	0	0
23	0	0	0	0	0
24	0	0	0	0	0

1.2 Определение основных размеров кулачкового механизма

Для кулачковых механизмов с поступательно движущимся толкателем основными размерами звеньев, определяющими величину угла давления и размеры механизма, являются:

а) минимальный радиус rmin кулачка;

б) смещение (дизаксиал) е – кратчайшее расстояние от оси вращения

кулачка до оси толкателя.

Минимальный радиус rmin кулачка определяется из условия ограничения угла давления. Для любого положения механизма текущий угол давления не должен превышать максимально допустимое значение βadm. Основные размеры кулачкового механизма можно определить графически, решая условие незаклинивание механизма:

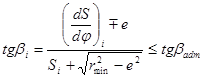
Так как дизаксиал е и допускаемое значение βadm заданны, то можно найти rmin (рис.2). мм – минимальный радиус кулачка.

1.3 Построение теоретического профиля кулачка

Построение профиля кулачка проводится методом обращенного движения: всему механизму сообщается вращение вокруг оси кулачка с угловой скоростью – ω, равной и обратнонаправленной угловой скорости ω кулачка.

Тогда по отношению к неподвижной системе координат кулачек остановится, а толкатель будет совершать плоскопараллельное движение.

Из произвольной точке проводим окружности радиусами rmin и е в принятом масштабе М 2:1. Окружность радиусом е разбиваем на n=24 частей в направлении против хода часовой стрелки, так как дизаксиал отрицательный. Из полученных точек проводим полукасательные по вращению кулачка. Эти полукасательные есть положение оси толкателя в обращенном движении. В принятом масштабе М отложим от точек пересечения полукасательных с окружностью радиусом rmin во внешнюю сторону отрезки Si, соответствующие перемещению толкателя для данного положения кулачка по таблице 1. Соединив полученные точки, получим теоретический профиль кулачка.

1.4 Выбор радиуса ролика

Построение практического профиля кулачка.

Радиус ролика rр выбирается из условий наименьших контактных напряжений и обеспечения реальных размеров кулачка:

rр≤0,7ρmin; rр≤0,4rmin, где ρmin – минимальный радиус кривизны теоретического профиля кулачка.

ρmin=42 мм, следовательно, должно быть rр≤29,4 мм и rр≤18,68 мм.

Из таблицы 4 [1] выбираем в качестве ролика радиальный шарикоподшипник сверхлегкой серии с радиусом

rр=D/2

и радиусом оси

r=d/2

1000904, D=37 мм, d=20 мм, rp=18,5 мм, r=9,25 мм.

Практический профиль кулачка получается, если теоретический уменьшить на величину радиуса ролика rр. Для этого из точек на теоретическом профиле проводят окружности радиусом rр и по внутренней огибающей этих окружностей проводят линию, которая является практическим профилем кулачка.

1.5 Расчет толщины кулачка

Для нормальной работы кулачкового механизма необходимо выполнения условия контактной прочности:

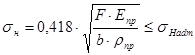, где

F – сила взаимодействия толкателя и кулачка [Н];