Курсовая работа: Багатокритеріальна задача лінійного програмування
X* j – вектор, що оптимальний для j - ої функції мети;
Всі ці міри неоптимальності складають квадратну матрицю, рядки якої відповідають k оптимальним векторам X* i для кожної функції мети, а стовпці – k функціям мети Cj . Ця матриця розглядається як платіжна матриця матричної гри двох партнерів X* і Z , що визначена множиною стратегій X*={X*1 , …, X*k } першого гравця, і Z={C1 X, …, Ck X} другого. Всі міри неоптимальності є недодатними, і є коефіцієнтами програшу першого гравця. На головній діагоналі вони рівні нулю (бо є мірами неоптимальності оптимального вектора для своєї ж функції).
3) Матриця мір неоптимальності заміняється еквівалентною їй матрицею додаванням до кожної міри неоптимальності 
, тобто найбільшого з абсолютних значень всіх мір. Якщо таке найбільше значення рівне нулю, то всі міри рівні нулю, і в такому випадку замість нього до усіх мір додається число 1. В результаті отримуємо матрицю з невід’ємними елементами. На головній діагоналі усі вони рівні максимальному значенню. Така заміна матриці не змінює рішення гри, змінює тільки її ціна. Тобто тепер гра має вигляд не гри програшів, а гри з пошуком максимального виграшу. Для пошуку оптимальної стратегії для першого гравця гра подається як пара взаємнодвоїстих однокритеріальних задач ЛП. Для першого гравця потрібні значення змінних двоїстої задачі 
:
| v1 = | v2 = | … | vk = | W= | ||
- | - | … | - | 1 | ||
| -u1 |  = |  |  | … |  | 1 |
| -u2 |  = |  |  | … |  | 1 |
| … | … | . | . | . | . | . |
| -uk |  = |  |  | … |  | 1 |
| 1 | Z = | -1 | -1 | … | -1 | 0 |
Розв’язавши цю задачу і отримавши оптимальні значення max(Z) = min(W) , що досягаються при значеннях змінних двоїстої задачі 
, можна обчислити вагові коефіцієнти 
для компромісного розв’язку багатокритеріальної задачі:
, 
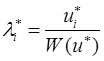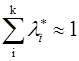
Компромісний вектор значень змінних для багатокритеріальної задачі є лінійною комбінацією оптимальних векторів кожної функції мети. Це сума векторів, що помножені кожен на свій ваговий коефіцієнт:
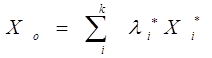
Підставивши цей компромісний вектор в кожну функцію мети багатокритеріальної задачі отримуємо компромісні значення цих функцій.
3. Вирішування
Рівняння, нерівності та функції записуються у таблицю:
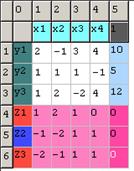
Розв’язування задачі ЛП для кожної функції мети окремо:
Пошук оптимального розв’язку для функції Z1
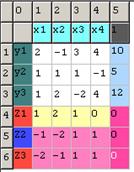
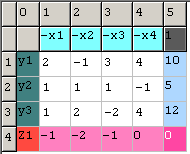
Задача для симплекс-метода з функцією Z1
Незалежних змінних немає.
Виключення 0-рядків: немає.
Опорний розв’язок: готовий (усі вільні члени невід’ємні).
Пошук оптимального розв’язку:
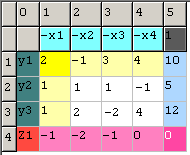
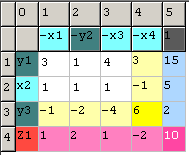
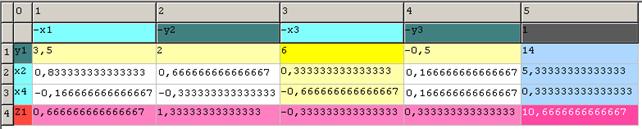
Результат для прямої задачі:
У рядку-заголовку:
– x1 = 0;
– y2 = 0;
– y1 = 0;
– y3 = 0;
У стовпці-заголовку:
x3 = 2,33333333333333;
x2 = 4,55555555555556;