Курсовая работа: Дискретное программирование

где D — конечное множество.

Алгоритм является итеративным, и на каждой итерации происходит работа с некоторым подмножеством множества D. Назовем это подмножество текущим и будем обозначать его как D(q), где q — индекс итерации. Перед началом первой итерации в качестве текущего множества выбирается все множество D (D(1)=D), и для него некоторым способом вычисляется значение верхней оценки для целевой функции max f(x) ≤ ξ( D(1)). Стандартная итерация алгоритма состоит из следующих этапов:

1) если можно указать план x(q)<D(q), для которого f(x(q))≤ξ( D(q)), то x(q)=х* — решение задачи (*).

2) если такой план не найден, то область определения D(q) некоторым образом разбивается на подмножества D1(q), D2(q), ..., Dlq(q), удовлетворяющие условиям:

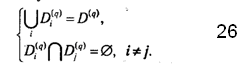
Для каждого подмножества находятся оценки сверху (верхние границы) для целевой функции ξD1(q), ξD2(q), ..., ξDl1(q), уточняющие ранее полученную оценку ξD(q), то есть ξDi(q) ≤ ξD(q), i<1:lq. Возможно одно из двух:

2.1) если существует такой план х(q), что то этот план оптимальный.

2.2) если такой план не найден, то выбирается одно из множеств Di(q), i>1:lq (как правило, имеющее наибольшую оценку.

Все имеющиеся к текущему моменту концевые подмножества, т. е. те подмножества, которые еще не подверглись процессу дробления, переобозначаются как D1(q+1), D2(q+1),..., Dl(q+1)(q+1), после чего процесс повторяется.

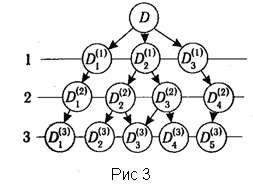
Схема дробления множества D представлена на рис.3 в виде графа. Существуют и более сложные системы индексации подмножеств, при которых не требуется их переобозначение на каждом шаге.

Конкретные реализации метода ветвей и границ связаны с правилами разбиения на подмножества (правилами ветвления) и построения оценок значений целевых функций на данных подмножествах (границ).

5.2 Решение ЦЗЛП методом ветвей и границ

Рассмотрим применение алгоритма метода ветвей и границ для решения ЦЗЛП (4.2)-(4.3). Как уже упоминалось, через D(q) обозначается подмножество множества допустимых планов задачи. Перед началом первой итерации (q = 1) в качестве текущего множества берется все множество D (D(1) = D), после чего решается стандартная задача линейного программирования (D(1), f). Нетрудно заметить, что она является непрерывным аналогомисходной задачи 2-3.

Если найденный оптимальный план (1) содержит только целочисленные компоненты, то он является и оптимальным планом для 2-3: (1) = x*. В противном случае значение f((1)) становится оценкой (верхней границей) значения целевой функции на множестве D(1), и мы переходим к выполнению стандартной итерации алгоритма. Опишем входящие в нее этапы.

1) Выбирается некоторая нецелочисленная компонента плана k(q). Поскольку в оптимальном плане она должна быть целой, то можно наложить ограничения xk ≤ [k(q)] и xk ≥ [k(q)]+1. Таким образом, D(q) разбивается на подмножества

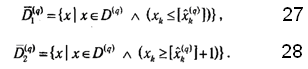
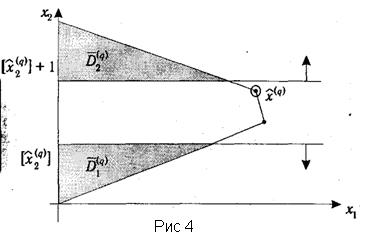
Графическая интерпретация такого разбиения множества D(q) приведена на рис.4.

2) Решаются задачи линейного программирования

Соответствующие максимальные значения целевой функции принимаются как ее оценки на этих множествах:

Если оптимальный план для одной из решенных задач удовлетворяет условию

и содержит только целые компоненты, то, значит, найдено решение основной задачи 2-3. В противном случае среди всех концевых подмножеств, полученных как на предыдущих (Di(q)), так и на текущем (D1(q), D2(q)) этапе, выбирается область с наибольшей оценкой ξ(Di(q)). Она становится текущим рассматриваемым подмножеством (D(q+1)). Далее производится перенумерация концевых множеств и вычислительный процесс итеративно повторяется.