Для системы связи (СС) с переспросом с ожиданием ответа одностороннего действия (рис. 1) при заданных исходных данных:

1. Найти двоичный циклический (n,k)-код Хэмминга, который обеспечивает передачу сообщений в СС с вероятностью выдачи ложного сообщения Р_{лс( n , k )} < P_доп при следующих условиях:

¾ прямой дискретный канал в СС является двоичным симметричным каналом (ДСК) с постоянными параметрами;

¾ обратный непрерывный канал – без помех;

¾ код используется только для обнаружения ошибок;

¾ найденный значения n и k должны обеспечивать минимум разности P_доп -Р_{лс( n , k )} для возможных значений n и k.

2. Отложить в координатных осях вычисленные значения Р_{лс( n , k )} для всех исследованных пар (n,k). В этих же осях прямой линией изобразить заданное значение P_доп .

Исходные данные для курсовой работы (вариант №22):

Вероятность искажения двоичного символа p	6x10-4
Допустимая вероятность ложного сообщения Pдоп	2x10-7
Допустимое число переспросов s	∞
Разрядность кода n	>10
Порождающий многочлен gi (x)	g3 (x)
Тип кодера	КД 1
Ввод информационных символов в кодер	последовательно
Тип декодера	ДК 2

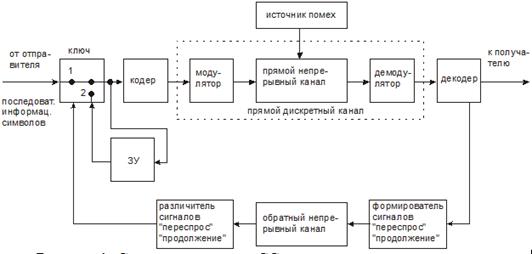
Рисунок 1. Структурная схема СС с переспросом с ожиданием ответа одностороннего действия

Описание работы СС с переспросом с ожиданием ответа одностороннего действия (рис. 1):

Информационная последовательность отдельными комбинациями не корректирующего кода через первое положение ключа направляется в кодер и в ЗУ передатчика. На выходе кодера образуется комбинация корректирующего кода, которая поступает в модулятор прямого канала. В прямом канале возможно искажение сигнала. На приемной стороне решение о принятом символе принимается демодулятором с так называемой зоной ненадежности.

Принцип его работы можно понять из рисунка.

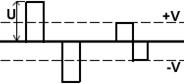
Пусть символ «1» передается по каналу связи импульсом положительной полярности с амплитудой U, а «0» импульсом отрицательной полярности с той же амплитудой.

В демодуляторе выделена некоторая зона +V –V, если принимаемый импульс попадает в эту зону (зона ненадежности), то демодулятор считает, что он не может принять надежного решения, о том, какой символ передавался. В этом случае, демодулятор выдает символ ненадежности Z. С выхода демодулятора комбинации поступают на вход декодера. После поступления всей комбинации с выхода декодера в обратный канал направляется одна из двух команд:

¾ «переспрос», если содержатся ошибки в принятой комбинации, и одновременно кодовое слово с символами Z стирается;

¾ «продолжение», если не обнаружено ошибок, и комбинация не корректирующего кода направляется к получателю.

Если различитель команд получает команду «продолжения», то из ЗУ передатчика в прямой канал направляется следующая порция* информации. Если различитель команд получает команду «переспрос», то он переключает ключ в положение 2 и из ЗУ передатчика в прямой канал повторно направляется комбинация, которая была стерта.

После выдачи в прямой канал из ЗУ передатчика очередной порции информации, следующая порция не передаётся до тех пор, пока не будет получен ответ по этой порции.

Порядок расчета Р_лс и пример расчета Р_лс для циклического ( n , k )–кода Хэмминга, обеспечивающего минимум разности Р_доп – Р_{лс( n , k )} :

Произведем расчет для (18,13)-кода с d=3.

Для этого введем обозначения:

· P_бо – вероятность появления на выходе ДСК комбинации (n,k)-кода без ошибок при однократной передаче;

· Р_оо – вероятность появления на выходе ДСК комбинации (n,k)-кода с обнаруживаемыми ошибками при однократной передаче;

· Р_но – вероятность появления на выходе ДСК комбинации (n,k)-кода с необнаруживаемыми ошибками при однократной передаче;

· Р_{i £ v о} – вероятность появления на выходе ДСК комбинации с ошибками кратности i£v₀ ;

· Р_{i > v о} – вероятность появления на выходе ДСК комбинации с ошибками кратности i>v₀ , которые расположены так, что обнаруживаются кодом;

· Р_лс – вероятность появления на выходе СС с неограниченным числом переспросов ложного сообщения.

Найдем:

хэмминг код цикличный программа

P_бо = qⁿ , где q=1-p;

--> ЧИТАТЬ ПОЛНОСТЬЮ <--