Курсовая работа: Двойные звезды
Таким образом, известно три типа двойных звезд: визуально-двойные, спектрально-двойные и затменно-двойные. Изучение звезд, входящих в каждый из этих типов, имеет очень важное значение уже потому, что до сих пор только двойные звезды (и, конечно, Солнце) служат источником наших знаний о звездных массах. [6,12]
С эволюционной точки зрения ДЗ делят на тесные и широкие. Тесными двойными называют системы, в которых компоненты на некотором этапе жизни способны обмениваться веществом. А у широких двойных систем расстояние между компонентами так велико, что они не оказывают друг на друга иного влияния, кроме гравитационного. [10]
1.1.Физические и оптические визуально-двойные звезды.
Двойные звезды, у которых обнаружено орбитальное движение обоих компонентов вокруг общего центра масс, называются физическими двойными ; звезды, у которых наблюдаемая близость компонентов происходит оттого, что эти компоненты, находясь на совершенно различных от нас расстояниях, расположены почти в точности по одному лучу зрения, называются оптическими двойными . В некоторых случаях взаимное линейное расстояние между компонентами физической двойной звезды настолько велико (например, третий компонент звезды Капелла из созвездия Возничего, находящийся на расстоянии 12' от двух ярких компонентов), что их орбитальные движения происходят чрезвычайно медленно. В таком случае судить о том, представляет ли данная двойная звезда физическую или оптическую двойную, можно на основе сравнения собственных движений ее компонентов. Если эти собственные движения близки друг к другу и по величине, и по направлению, значит, двойная звезда физическая, в противном случае–оптическая.
Орбитальное движение физических двойных звезд можно изучать, определяя изменениеэкваториальных координат обоих компонентов, происходящее с течением времени. Для этой цели можно пользоваться так называемыми абсолютными методами, так и дифференциальными методами. Однако проще и точнее можно изучать относительное движение компонентов. С этой целью один из компонентов (обычно более яркий, называемый главной звездой) принимают за неподвижный и изучают относительное движение другого компонента (менее яркого, называемого спутником). При этом с помощью окулярного микрометра или по фотографическому снимку измеряют две величины: расстояние между компонентами, обозначаемое буквой р. и выражаемое в секундахдуги, так называемый позиционный угол Q между направлением от главной звезды к северному полюсу мира и линией,соединяющей главную звезду со спутником. Угол Q отсчитывается от направления к полюсу мира против хода часовой стрелки от 0 до 360°.
Если повторять такие измерения одной и той же двойной звезды спустя достаточно продолжительные промежутки времени, можно, получив ряд положений спутника относительно главной звезды, определить сначала видимую, а затем и истинную орбиты спутника.
 |
????????? ?? ??????? ????? ??????????? ??????? ?????????? ??????? ???????? ? ??????? ???????????. ???, ? ??????? ?????? g ????????? ??????? ?????? ?????????, ? ??????? ???????. ? ??????? h ????????? ??????? ?????? ??????, ? ??????? ?????????? ? ?. ?. ????? ??????? ? ??????? ??????????? ??????? ??????? ????????? ???????????????? ????????? (??????????????) ? ???? ??????? ??????? ?? ??????????????? ???????? ????? ???????????.
Видимые орбиты, спутников визуально-двойных звезд всегда имеют форму эллипса (рис. 2). Однако главная звезда обычно оказывается не в фокусе такого эллипса. Происходит это вследствие того, что истинная орбита спутника рассматривается земным наблюдателем наискось и видимая орбита представляет собой ее проекцию на плоскость, перпендикулярную к лучу зрения. И только в тех редких случаях, когда эта плоскость совпадает с плоскостью истинной орбиты, видимая и истинная орбиты тоже совпадают и главная звезда оказывается в фокусе видимой орбиты спутника.
Построив видимую орбиту, можно определить истинную орбиту. Для этого обычно находят следующие 7 элементов истинной орбиты: T – период обращения, выраженный в годах; t – момент прохождения спутника через периастр (ближайшую к главной звезде точку истинной орбиты); е – эксцентриситет; а – большуюполуось орбиты, выраженную в секундах дуги; i –наклонение орбиты, т.е. угол наклона плоскости орбиты к плоскости, перпендикулярной лучу зрения; d – позиционный угол одного из узлов орбиты, т. е. тех двух ее точек, в которых она пересекает плоскость, проходящую через главную звезду и перпендикулярную лучу зрения (обычно берется тот позиционный угол, который меньше 180°); w – угол в плоскости орбиты от узла до периастра, считаемый в направлении движения спутника. [4,11]
Значительно сложнее обстоит дело с определением орбит кратных звезд в тех случаях, когда три (или более) компонента находятся друг от друга на сравнительно небольших расстояниях, и приходится, таким образом, иметь дело с задачей трех тел.
Третий закон Кеплера в форме, полученной Ньютоном для случая движения спутника относительно центрального тела, дает следующее выражение для суммы масс центрального тела и спутника:
![]() , (1.1)
, (1.1)
где k 2 – гравитационная постоянная, a – большая полуось орбиты спутника, а T – период его обращения.
Применим выражение для определения суммы масс компонентов визуально-двойной звезды и напишем подобное выражение для суммы масс Солнца ![]() и Земли
и Земли ![]() :
:
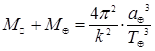 , (1.2)
, (1.2)
где ![]() – астрономическая единица, а
– астрономическая единица, а ![]() – период обращения Земли вокруг Солнца, т. е. звездный год.
– период обращения Земли вокруг Солнца, т. е. звездный год.
Разделим выражение (1.1) на (1.2), пренебрегая массой Земли из-за ее малости, получим:
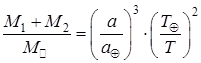 . (1.3)
. (1.3)
Зная величину отношений ![]() и
и ![]() , можно по формуле (1.3) вычислить, во сколько раз сумма масс компонентов двойной звезды больше массы Солнца.
, можно по формуле (1.3) вычислить, во сколько раз сумма масс компонентов двойной звезды больше массы Солнца.
Если принять за единицу длины астрономическую единицу, за единицу времени – звездный год (время полного оборота Земли вокруг Солнца) и за единицу массы – массу Солнца, выражение принимает очень простой вид:
![]() . (1.4)
. (1.4)
Период Т является одним из семи элементов истинной орбиты, а большая полуось а связана следующим очевидным соотношением с большой полуосью истинной орбиты ![]() , выраженной в секундах дуги и с параллаксом p :
, выраженной в секундах дуги и с параллаксом p :
![]() . (1.5)
. (1.5)
Если за единицу длины принять астрономическую единицу, то
![]() . (1.6)
. (1.6)
Таким образом, будем ли мы для вычисления масс пользоваться формулами или более простыми формулами в обоих случаях, кроме элементов орбиты ![]() и Т , необходимо знать также и параллакс звезды p .
и Т , необходимо знать также и параллакс звезды p .
1.2.Спектрально-двойные звезды.
Звезды, двойственность которых устанавливается лишь на основании спектральных наблюдений, называются спектрально – двойными.
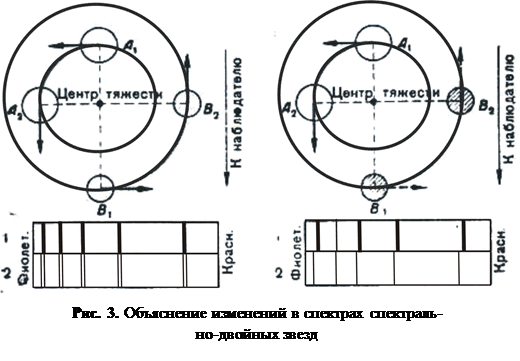
Характер и причина изменения спектров спектрально-двойных звезд объясняются рис.3. Если очень близкие компоненты двойной звезды, движущиеся вокруг общего центра масс, мало отличаются друг от друга по спектру и по бле ску, то в спектре такой звезды должно наблюдаться периодически повторяющееся раздвоение спектральных линий.
ску, то в спектре такой звезды должно наблюдаться периодически повторяющееся раздвоение спектральных линий.
Если один компонент занимает положение А1 , а другой – положение В1 , то оба они будут двигаться под прямым углом к лучу зрения, направленному к наблюдателю, и раздвоения спектральных линии не получится. Но если компоненты занимают положение А2 и В2 , то компонент А - движется к наблюдателю, а компонент В – от наблюдателя и раздвоение спектральных линий наблюдаться будет, так как у первого компонента спектральные линии сместятся к фиолетовому концу спектра, а у второго – к красному концу. Затем при дальнейшем движении компонентов раздвоение спектральных линий постепенно исчезнет (оба компонента будут опять двигаться под прямым углом к лучу зрения) и снова повторится, когда компонент А будет двигаться от наблюдателя, а компонент В – к наблюдателю. Таким образом, спектральные линии компонентов А и В будут колебаться около некоторых средних своих положений, при которых они будут совпадать и которые соответствуют лучевой скорости центра масс системы.
 |
? ?????? ??, ???? ???? ?? ??????????? ??????????? ???????? ?? ?????? ??????? (?????? ????? ???. 3), ?????????? ???????????? ????? ??????????? ?? ????? (??-?? ???????? ??????? ????????), ?? ????? ??????? ??????? ?????? ?????????? ????? ??? ??, ??? ? ? ?????? ??????.
 |
??????? ?????????, ???????????? ? ???????? ???????????-??????? ?????, ????????, ?????????? ? ????????? ?? ?????????, ?????? ?????? ????????. ???????? ???????? ?? ????????? ???????? 2,4Ч (g ????? ?????????), ? ???????? ??????? ? ??????? ???.
Для определения элементов орбиты какой-либо спектрально-двойной звезды необходимо иметь достаточно большое количество спектрограмм этой звезды, дающих возможность построить так называемую кривую лучевых скоростей. При построении этой кривой по оси абсцисс откладывается время, а по оси ординат – лучевые скорости. Форма кривой лучевых скоростей зависит только от двух элементов – эксцентриситета е и угла w , определяющего положение периастра. Характерные образцы кривых лучевых скоростей для некоторых частных значений е и w изображены на рисунке 4. Положение горизонтальной прямой у всех кривых этого рисунка соответствует лучевой скорости, которую компоненты имеют при своем движении под прямым углом к лучу зрения (т.е., иными словами, лучевой скорости центра масс системы).
Независимо от применяемого способа из числа элементов орбит спектрально-двойных звезд могут быть определены только w , ![]() , Т и t . Совершенно нельзя определить позиционный угол и нельзя определить в отдельности наклонение i плоскости орбиты и большую полуось а , так как одни и те же лучевые скорости могут получиться при движении звезды по орбитам с различными наклонениями и соответственно большими различными полуосями. [4,5,12]
, Т и t . Совершенно нельзя определить позиционный угол и нельзя определить в отдельности наклонение i плоскости орбиты и большую полуось а , так как одни и те же лучевые скорости могут получиться при движении звезды по орбитам с различными наклонениями и соответственно большими различными полуосями. [4,5,12]
1.3.Затменно-двойные звезды.
Затменными переменными называются неразрешимые в телескопы тесные пары звезд, видимая звездная величина которых меняется вследствие периодически наступающих для земного наблюдателя затмений одного компонента системы другим. В этом случае звезда с большей светимостью называется главной, а с меньшей – спутником. Типичными примерами звезд этого типа являются звезды Алголь (b Персея) и b Лиры. Вследствие регулярно происходящих затмений главной звезды спутником, а также спутника главной звездой суммарная видимая звездная величина затменных переменных звезд меняется периодически.
Разность звездных величин в минимуме и максимуме называется амплитудой, а промежуток времени между двумя последовательными максимумами или минимумами – периодом переменности. У Алголя, например, период переменности равен 2d 20h 49m , а у b Лиры– 12d 21h 48m . По характеру кривой блеска затменной переменной звезды можно найти элементы орбиты одной звезды относительно другой, относительные размеры компонентов, а в некоторых случаях даже получить представление об их форме.
На рис. 5 показаны кривые блеска некоторых затменных переменных звезд вместе с полученными на их основании схемами движения компонентов. На всех кривых заметны два минимума: глубокий (главный, соответствующий затмению главной звезды спутником), и слабый (вторичный), возникающий, когда главная звезда затмевает спутник.
 |
?? ????????? ?????????? ???????? ?????? ?????? ????? ???????? ????????? ?????? ? ??????????? ????????? ?????????? ?????:
1. Характер затмений (частное, полное или центральное) определяется наклонением i и размерами звезд. Когда i = 90°, затмение центральное, как у b Лиры (рис. 5). В тех случаях, когда диск одной звезды полностью перекрывается диском другой, соответствующие области кривой блеска имеют характерные плоские участки (как у IH Кассиопеи), что говорит о постоянстве общего потока излучения системы в течение некоторого времени, пока меньшая звезда проходит перед или за диском большей. В случае только частных затмений минимумы острые (как у RX Геркулеса или b Персея).
2. На основании продолжительности минимумов находят радиусы компонентов R 1 и R 2 , выраженные в долях большой полуоси орбиты, так как продолжительность затмения пропорциональна диаметрам звезд.
3. Если затмение полное, то по отношению глубин минимумов можно найти отношение светимостей, а при известных радиусах,– также и отношение эффективных температур компонентов.