Курсовая работа: Эффект магнитоимпеданса

1.1 Эффект магнитного импеданса

Явление магнитного импеданса было открыто более 70 лет назад в работах Е.П. Харрисона с соавторами, выполненных на железо-никелевых проволоках. Термин «магнитный импеданс» не использовался ни в этих первых публикациях, ни в первых расчетах проведенных позднее.

В 1991г. В.Е. Махоткин с соавторами создали высокочувствительный датчик малых магнитных полей с чувствительным элементом в виде аморфной ленты FeCoSiB, который работал на принципе изменения импеданса под воздействием внешнего магнитного поля. Авторы этой работы, посвященной созданию конкретного прототипа датчика магнитных полей, не обсуждали причины возникновения эффекта и термин «магнитный импеданс» не использовали.

Не был термин «магнитный импеданс» введен и в ранних работах группы К. Мори, ставших предвестниками открытия заново явления магнитоимпеданса в 1994г.

Хотя уже первые эксперименты, в которых наблюдалось изменение импеданса пермаллоевых проволок при приложении внешнего поля, были объяснены на основе классического скин-эффекта и зависимости глубины скин-слоя от величины эффективной магнитной проницаемости, Е.П. Харрисон с соавторами так и не добились повторяемости результатов. Позднее появились более совершенные технологии производства материалов с высокой магнитной проницаемостью, которые обеспечили повторяемость результатов ГМИ-исследований и возможность контролируемой разработки ГМИ-материалов.[3]

ГМИ-образцы разрабатываются различными методами в виде проволок, лент, тонких пленок, многослойных пленочных структур и т.д. Имеются четыре группы магнитных материалов, в которых может наблюдаться ГМИ-эффект:

1. Аморфные сплавы с малым значением константы анизотропии. Среди них система Co-Fe-Si-B имеет небольшую отрицательную константу магнитострикции;

2. Нанокристаллические материалы типа Fe-Cu-Nb-Si-B, в которых размер зерен порядка 10нм;

3. Кристаллические сплавы с чрезвычайно низкой кристаллической анизотропией и низкой магнитострикцией. Среди них – пермаллой (сплав никеля и железа) с высокой концентрацией никеля и с добавками Mo, Re, Ti;

4. Нанокомпозиты, состоящие из смеси однофазных частиц. Такими являются системы на основе Fe-B-N и Co-Cr-O. [6]

Для определения относительной величины эффекта ГМИ исследователи использовали следующее соотношение:

,(1)

где Z(H) – импеданс образца в магнитном поле Н, Z(H=H_нас ) – импеданс образца в магнитном поле насыщения, за которое принимается величина максимального внешнего поля, приложенного к образцу. В этом случае величина ∆Z/Z, которую принято называть ГМИ-отношением, всегда положительна, и может достигать значений, больших, чем 100 %.

В работах других авторов ГМИ-отношение рассчитывалось иначе:

,(2)

где Z(H=0) – величина импеданса образца в отсутствии внешнего магнитного поля. При таком подходе величина ГМИ-отношения может быть не только положительной, но и отрицательной.

Различают продольный и поперечный эффекты гигантского магнитоимпеданса [7]. Продольным эффектом принято называть эффект, возникающий при приложении внешнего магнитного поля параллельно направлению протекающего электрического тока. В свою очередь, поперечным эффектом принято называть эффект магнитоимпеданса, возникающий в случае, когда внешнее магнитное поле приложено перпендикулярно направлению протекания электрического тока.

Магнитоимпеданс обусловлен влиянием внешнего магнитного поля на распределение плотности переменного тока по сечению проводника, что связано с проявлением так называемого скин-эффекта. Толщина скин-слоя δ, или, иначе говоря, глубина проникновения переменного тока в объем проводника, определяется по формуле:

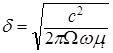,(3)

где с – скорость света в вакууме, Ω – проводимость, ω – циклическая частота переменного тока, μ_t – эффективная магнитная проницаемость.

Как известно, величина эффективной магнитной проницаемости во многом определяется доменной структурой и процессами ее перемагничивания. Внешнее постоянное магнитное поле Н, приложенное к проводнику, вызывает в нем процессы перестройки доменной структуры, и, следовательно, изменяет величину магнитной проницаемости μ_θ . Изменение величины μ_θ приводит к изменению глубины скин-слоя, по которому протекает высокочастотный электрический ток, что в свою очередь приводит к изменению импеданса ферромагнитного образца Z. Связь между импедансом образца Z и его эффективной магнитной проницаемостью может быть, в общем случае, представлена в виде:

Z ~(μ_θ f)^-1/2. (4)

Подобные рассуждения оправданы только для средних частот переменного тока и частот порядка десятков МГц, когда толщина скин-слоя δ намного меньше некоторого характерного размера проводника (радиус проволоки, толщина фольги).

На низких частотах, когда скин-эффект мал и плотность тока практически одинакова по всему сечению проводника, изменение импеданса в магнитном поле связывают с так называемым магнитоиндуктивным эффектом. Данный эффект обусловлен внутренней индуктивностью проводника L_i (μ_t ), которая, как и толщина скин-слоя, зависит от эффективной магнитной проницаемости μ_t . Импеданс проводника, определяемый магнитоиндуктивным эффектом, может быть записан в виде:

, (5)

В общем случае импеданс проводника будет определяться как магнитоиндуктивной составляющей, так и толщиной скин-слоя. Однако на высоких частотах магнитоиндуктивная компонента мала и для упрощения расчетов ей обычно пренебрегают.

Таким образом, для наблюдения ГМИ-эффекта необходимо, чтобы поперечная магнитная проницаемость имела большую величину и значительно изменялась во внешнем магнитном поле, то есть для существования ГМИ-эффекта принципиальным является магнитная мягкость материала.

Рассмотрим основные факторы, влияющие на эффект магнитного импеданса.