run(Start,End):-db0(Start,End), db(Start,End), db_path(Start,End,MP,MD),

write("Optimum way: "),write(MP),nl,

write("Length of an optimum way="),write(MD),

nl,nl.

path(A,Z,Path,C):- path1(A,[Z],0,Path,C).

path1(A,[A|Path1],C,[A|Path1],C).

path1(A,[Y|Path1],C1,Path,C):- arca(X,Y,CXY), not(member(X,Path1)),C2=C1+CXY, path1(A,[X,Y|Path1],C2,Path,C).

member(Head,[Head|_]).

member(Head,[_|Tail]):- member(Head,Tail).

db0(X,Y) :-path(X,Y,P,C), assert(db_path(X,Y,P,C)).

db(X,Y):-db_path(X,Y,P,C), path(X,Y,MP,MC), MC<C,!,

retract(db_path(X,Y,P,C)), assert(db_path(X,Y,MP,MC)), db(X,Y).

db(_,_).

6. Тестирование программы

а) Пусть имеем следующий граф:

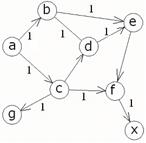Рис.2	Рис.2а

Ищем оптимальный путь из a в х , согласно графу оптимальный путь содержит следующие узлы: a c f x , что изображено на рис.2а.

Программа:

Данные ручного расчета и программы совпадают.

б) Изменим длину ребра a - c :

Рис.3	Рис.3а

Ищем оптимальный путь из a в х , согласно графу оптимальный путь содержит следующие узлы: a b e f x , что изображено на рис.3а.

Программа:

Данные ручного расчета и программы совпадают.

в) Изменим длину ребра b - d :

Рис.4	Рис.4а

Ищем оптимальный путь из a в х , согласно графу оптимальный путь содержит следующие узлы: a b d e f x , что изображено на рис.4а.

Программа:

Данные ручного расчета и программы совпадают.

Литература

1. И 57. Использование Турбо-Пролога: Пер. с англ.-М.:Мир, 1990.-410 с., ил.