Курсовая работа: Электрическое поле

При предельном переходе объем V и его поверхность S стягиваются в точку наблюдения, в которой вычисляется дивергенция. Согласно (1.4.1), поток напряженности E через любую бесконечно малую сферу, внутри которой нет зарядов, – тождественный нуль. Поэтому из (1.4.2) следует, что в точках с нулевой плотностью зарядов (r=0) дивергенция E равна нулю. Рассмотрев поток через малую сферу V вокруг точки, в которой дивергенция напряженности не равна нулю, можно показать с помощью (1.4.1) и (1.4.2) , что в такой точке объемный заряд есть, поэтому точки, в которых дивергенция напряженности отлична от нуля, являются источниками силовых линий.

В курсе математики доказывается теорема Остроградского-Гаусса (была установлена К. Гауссом в 1844 независимо от М.В. Остроградского, доказавшего ее в 1839):

. (1.4.3)

Здесь V – произвольный объем, ограниченный поверхностью S. Применим теорему (1.4.3) к потоку электростатического поля. С учетом (1.4.1) получим:

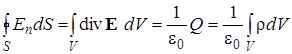. (1.4.4)

Из равенства интегралов ввиду произвольности объема V следует равенство подынтегральных выражений, т.е. теорема Гаусса в дифференциальной форме (А. Пуассон, 1850 г.):

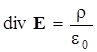. (1.4.5)

Из тех областей пространства, в которых дивергенция Е положительна, силовые линии Е исходят (r>0), в тех областях, где divE < 0 силовые линии заканчиваются (r<0), а через те области, где divE = 0 силовые линии проходят, но не рождаются и не исчезают, так как в этих областях r=0 (зарядов нет).

Циркуляция и ротор векторного поля. Градиент скалярной функции

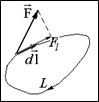
Циркуляция С_L произвольного векторного поля F(x,y,z) по замкнутому контуру L определяется следующим соотношением:

, (1.5.1)

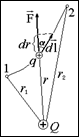
где F_l – проекция вектора F на направление элемента контура dl (см. рис. 1.5.1).

Ротор – это еще одно понятие из математической теории векторных полей. В декартовой системе координат (x,y,z) ротор F (обозначение «rotF») определяется как вектор, компоненты которого равны определенным комбинациям пространственных производных вектора F, именно:

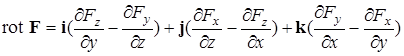(1.5.2)

Физический смысл ротора следует из равенства, доказываемого в курсе математики:

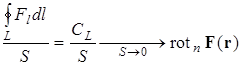. (1.5.3)

Здесь n – нормаль к площадке S, L – контур, ограничивающий эту площадки, который при этом предельном переходе стягивается в точку наблюдения . Если ротор векторного поля в некоторой точке наблюдения не равен нулю, то в любой достаточно малой окрестности этой точки силовые линии поля образуют микроскопические замкнутые контура вокруг нее («завихряются»). Поэтому область, где ротор векторного поля отличен от нуля, называют вихрем поля, а само поле, ротор которого отличен от нуля называется вихревым. Скорость движения потоков жидкости или газа, рассматриваемая как функция координат, является наглядным примером векторного поля. Турбулентности в жидкости или газе образуются именно вокруг точек, в которых отличен от нуля ротор скорости потока жидкости (газа). Изображение поля с помощью силовых линий в области пространства, где ротор отличен от нуля (точно так же, как и в точках с ненулевой дивергенцией), невозможно.

Как будет видно из дальнейшего, циркуляция и ротор электростатического поля, тождественно равны нулю во всем пространстве. Поэтому электростатическое поле – это относительно простое силовое поле. Такими же свойствами обладает и гравитационное поле.

Понятие градиента уже вводилось в курсе механики. Напомним его. Градиент функции f(x,y,z), зависящей от координат – это вектор, декартовы компоненты которого являются пространственными производными функции f :

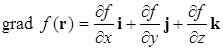. (1.5.5)

Пусть . Можно показать, что тогда необходимо и достаточно, чтобы ротор был равен нулю:

. (1.5.6)

Потенциальность электростатического поля. Электрический потенциал

Работа поля по переносу пробного q заряда из некоторой точки 1 в некоторую точку 2 не зависит от траектории его движения и определяется для данного поля и данного заряда только координатами этих точек. Для случая, когда источником поля является точечный заряд Q (рис. 1.6.1) это нетрудно обосновать следующим образом. Работа на элементарном отрезке траектории, по известному из механики определению, есть: . Раскрывая скалярное произведение векторов через угол a между ними, получаем

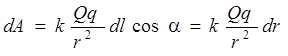. (1.6.1)