Використовуючи термостатовані камертонні генератори, можна досягти точності, на порядок чи два меншої. Їх можна використовувати й без подільників частоти.

Іноді для визначення рівності вимірюваної і зразкової частот як нуль-індикатор використовують телефонну трубку. Це зовсім простий метод, який не вимагає додаткової апаратури, треба лише, щоб величини напруг зразкової і контрольованої частот були достатніми (і безпечними) для телефонної трубки. Але користуватись цим методом доцільно тільки при порівнянні підвищених і високих частот, бо людське вухо нездатне сприймати звуки з частотою, нижчою за 12.15 Гц. Наявність такої "мертвої" зони при порівнянні частот порядку 1000.5000 Гц і вище майже не впливає на точність вимірювань, але при порівнянні частот порядку 40.60 Гц вона зовсім недоречна, бо суттєво зменшує точність порівняння.

2.2 Відношення двох частот

В універсальних цифрових частотомірах передбачена можливість вимірювання відношення двох частот: f_x і f_y . Сигнали вимірюваних частот подаються на формувачі імпульсів (рис.8), які формують імпульси з крутими фронтами для зменшення похибки від дрейфу рівнів спрацювання.

Якщо одна з частот набагато більша за іншу (f_x >>f_y ), то імпульс тривалістю Т_у з виходу формувача (рис.8, а) відкриває ключ і імпульси тривалістю Т_х надходять на вхід лічильника імпульсів упродовж часу Т_у . Числовий відлік лічильника імпульсів дорівнюватиме:

Якщо ж частоти f_x і f_y близькі за значенням, то імпульси з частотою f_y після формувача (рис.8, б) подаються на подільник частоти з коефіцієнтом ділення n. Числовий відлік лічильника імпульсів у такому разі дорівнюватиме:

Рис.8

Відсотковий частотомір. Сигнал частотою f_x надходить на формувач імпульсів (рис.9), який формує імпульси нормованої амплітуди з крутими фронтами. Сформовані імпульси подаються на подільник частоти з коефіцієнтом ділення n₁ . З вихідного сигналу подільника частоти формується імпульс тривалістю T₁ =n₁ T_x =n₁ /f_x , Генератор стабільної частоти f₀ і другий подільник частоти з коефіцієнтом ділення n₂ формують другий імпульс тривалістю Т₂ =n₂ Т₀ =n₂ /f₀ . Обидва імпульси подаються на ключ, який влаштований так, що він відкритий упродовж часу ΔТ=Т₂ -Т₁ . За час ΔТ на вхід лічильника імпульсів через ключ проходять імпульси з періодом Т₀ . Покази лічильника в кінці вимірювання становлять:

Рис.9

Якщо виконати умову

де f_хном - номінальне значення частоти, то

Якщо f_x близька до f_хном і n₂ =100, то N_x виражатиме наближено відхилення частоти від номінального значення у відсотках.

2.3 Похибки вимірювання частоти і інтервалів часу

Вимірювання частоти і інтервалів часу супроводжується такими складовими похибок вимірювання: похибка квантування; похибка, зумовлена нестабільністю частоти генератора кванту вальних імпульсів; похибка від нестабільності порогів спрацювання формувачів імпульсів.

Похибка квантування. Якщо генератор квантувальних імпульсів синхронізований з початком вимірюваного інтервалу часу (рис.10, а), то похибка квантування Δtвиникає в кінці вимірюваного інтервалу як різниця між результатом вимірювання N_x T₀ і вимірюваним інтервалом Т_х :

Δt=N_x T₀ -T_x .

Оскільки вимірювана величина до вимірювання невідома, то кінець інтервалу Т_х може з однаковою ймовірністю припасти на будь-який момент між сусідніми квантувальними імпульсами, тому похибку квантування Δtвважають випадковою і розподіленою за рівномірним несиметричним законом з граничним значенням Т₀ (рис.10, б). Математичне сподівання похибки квантування дорівнює T₀ /2, а середнє квадратичне відхилення σ=Т₀ /√12. Синхронізувати генератор квантувальних імпульсів з початком вимірюваного інтервалу Т_х часто не вдається, тому похибка квантування виникає на початку Δt₁ і в кінці Δt₂ вимірюваного інтервалу часу Т_х (рис.11). Похибки Δt₁ і Δt₂ розподілені за рівномірними несиметричними законами з граничним значенням Т₀ . Сумарна похибка квантування Δt=Δt₁ +Δt₂ розподілена за трикутним законом (законом Сімпсона) з граничним значенням Т₀ . Математичне сподівання сумарної похибки квантування дорівнює нулю, а середнє квадратичне відхилення σ=Т₀ /√6.

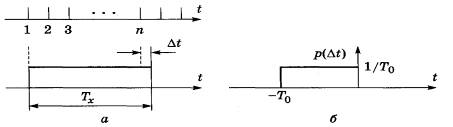
Рис.10

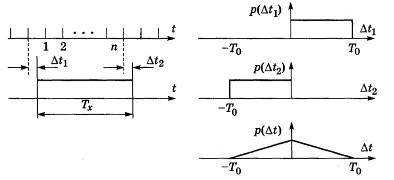
Рис.11

Відносна гранична похибка квантування під час вимірювання частоти за визначений інтервал часу Т_N дорівнює:

Отже, відносна гранична похибка квантування збільшується із зменшенням частоти. Для розширення частотного діапазону частотомірів у зону нижніх частот вдаються до таких заходів: