Курсовая работа: Элементы биомеханики

Работа отдельных элементов зависит от скорости нагрузки общего элемента.

Для упругой деформации выполняется закон Гука:

Откуда

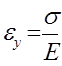
Скорость упругой деформации будет:

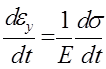(1)

Для вязкой деформации:

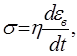
тогда скорость вязкой деформации будет:

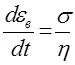(2)

Общая скорость вязко-упругой деформации равна сумме скоростей упругой и вязкой деформаций.

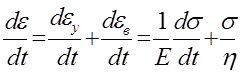(3)

Это есть дифференциальное уравнение модели Максвелла.

Вывод уравнения ползучести биоткани. Если к модели приложить силу, то пружина мгновенно удлиняется, а поршень движется с постоянной скоростью. Таким образом, на данный модели реализуется явление ползучести. Если F=const, то возникающее напряжение σ=const, т.е. 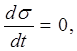тогда из уравнения (3) получим:

, отсюда

- уравнение ползучести биоткани.

Представим график ползучести:

Вывод уравнения релаксации напряжения в биотканях.

Если модель Максвелла растянуть и закрепить, то пружина начнет сокращаться. Со временем будет происходить релаксация, т.е. уменьшение напряжения. Если ε=const, то тогда уравнение (3) примет вид:

Решаем дифференциальное уравнение:

где σ₀ – начальное напряжение.