Курсовая работа: Физика сверхпроводимости
Отсюда по правилу Сильсби
Ic = 2рHcr . (3)
Возьмем Нс = 5·104 А/м и r = 0,1 см. Для такого образца Ic = 315A. Если учесть, что ток течет в поверхностном слое толщиной л (для Pbл≈400 Е = 4·10−8 м), то плотность сверхпроводящего критического тока
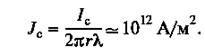 (4)
(4)
Для сверхпроводников 2-го рода правило Сильсби неприменимо. Критический ток в сверхпроводниках 2-го рода необычайно чувствителен к структуре образца и у одного и того же материала может меняться на несколько порядков величины.
2.3 Эффект Мейснера
В 1913г. немецкие физики Мейснер и Оксенфельд решили экспериментально проверить, как именно распределяется магнитное поле вокруг сверхпроводника. Результат оказался неожиданным. Независимо от условий проведения эксперимента магнитное поле внутрь проводника не проникало. Поразительный факт заключался в том, что сверхпроводник, охлажденный ниже критической температуры в постоянном магнитном поле, самопроизвольно выталкивает это поле из своего объема, переходя в состояние, при котором магнитная индукция В=0, т.е. состояние идеального диамагнетизма. Это явление получило название эффекта Мейснера.
Многие считают, что эффект Мейснера, является наиболее фундаментальным свойством сверхпроводников. Действительно, существование нулевого сопротивления неизбежно следует из этого эффекта. Ведь поверхностные экранизирующие токи постоянны во времени и не затухают в не измеряющемся магнитном поле. В тонком поверхностном слое сверхпроводника эти токи создают свое магнитное поле, строго равное и противоположное внешнему полю. В сверхпроводнике эти два встречных магнитных поля складываются так, что суммарное магнитное поле становится равным нулю, хотя слагаемые поля существуют совместно, поэтому и говорят об эффекте «выталкивание» внешнего магнитного поля из сверхпроводника.
Пусть в исходном состоянии идеальный проводник охлажден ниже критической температуры и внешнее магнитное поле отсутствует. Внесем теперь такой идеальный проводник во внешнее магнитное поле. Поле в образец непроникает, что схематически изображено на рис. 1. Сразу по появлении внешнего поля на поверхности идеального проводника возникает ток, создающий, по правилу Ленца, свое собственное магнитное поле, направленное навстречу приложенному, и полное поле в образце будет равно нулю.
Это можно доказать используя уравнения Максвелла. При изменении индукции В внутри образца должно возникнуть электрическое поле Е:
![]() (5)
(5)
Где с - скорость света в вакууме. Но в идеальном проводнике R= 0, так как
E = j с,
где с — удельное сопротивление, которое в нашем случае равно нулю, j — плотность наведенного тока. Отсюда следует, что B =const, но поскольку до внесения образца в поле В = 0, то ясно, что В = 0 и после внесения в поле. Это можно интерпретировать еще и так: поскольку с =0, время проникновения магнитного поля в идеальный проводник равно бесконечно.
Итак, внесенный во внешнее магнитное поле идеальный проводник имеет В = 0 в любой точке образца. Однако того же состояния (идеальный проводник при Т <Тс во внешнем магнитном поле) можно достигнуть и другим путем: сперва наложить внешнее поле на «теплый» образец, а затем охладить его до температуры Т <Тс .
Электродинамика предсказывает для идеального проводника совершенно другой результат. Действительно, образец при Т>Тс имеет сопротивление и магнитное поле в него хорошо проникает. После охлаждения его ниже Тс поле останется в образце. Эта ситуация изображена на рис. 2.
Таким образом, кроме нулевого сопротивления сверхпроводники обладают еще одним фундаментальным свойством - идеальным диамагнетизмом. Исчезновение магнитного поля внутри связано с появлением незатухающих поверхностных токов в сверхпроводнике. Но магнитное поле не может быть вытолкнуто полностью, т.к. это бы означало, что на поверхности магнитное поле падает скачком от конечного значения В до нуля. Для этого необходимо, чтобы по поверхности протекал ток, бесконечной плотности, что невозможно. Следовательно, магнитное поле проникает в глубь сверхпроводника, на некоторую глубину л.
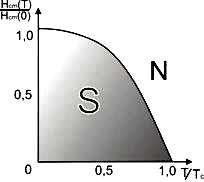
Эффект Мейснера Ї Оксенфельда наблюдается только в слабых полях. При увеличении напряженности магнитного поля до величины Н cm сверхпроводящее состояние разрушается.Это поле получило название критического Н cm .Зависимость между критическим магнитным полем и критической температурой хорошо описывается эмпирической формулой (6).
Н cm (T)= Н cm (0) [1-(T/Tc )2 ](6)
Где Н cm (0) – критическое поле экстраполированное к абсолютному нулю.
График этой зависимости приведен на рисунке 3. Этот график также можно рассматривать, как фазовую диаграмму, где каждая точка серой части соответствует сверхпроводящему состоянию, а белой области - нормальному.
По характеру проникновения магнитного поля сверхпроводники делятся на сверхпроводники первого и второго рода. В сверхпроводник первого рода магнитное поле не проникает до тех пор пока, напряженность поля не достигнет значения Н cm . Если поле превышает критическое значении, то сверхпроводящее состояние разрушается и поле полностью проникает в образец. К сверхпроводникам первого рода относятся все химические элементы сверхпроводники, кроме ниобия.
Подсчитали, что при переходе металла из нормального состояния в сверхпроводящее производится некоторая работа. Что, собственно, является источником этой работы? То, что у сверхпроводника энергия ниже, чем у того же металла в нормальном состоянии.
Ясно, что «роскошь» эффекта Мейснера сверхпроводник может себе позволить за счет выигрыша в энергии. Выталкивание магнитного поля будет иметь место до тех пор, пока связанное с этим явлением увеличение энергии компенсируется более эффективным ее уменьшением, связанным с переходом металла в сверхпроводящее состояние. В достаточно магнитных полях энергетически более выгодным оказывается не сверхпроводящее, а нормальное состояние, в котором поле свободно проникает в образец.
2.4 Глубина проникновения. Уравнение Лондонов
В 1935г. физики братья Лондоны предприняли попытку количественного описания электрических и магнитных свойств сверхпроводников. Предложенные ими уравнения имеют для сверхпроводников такое же значение, какое имеет закон Ома для нормальных проводников. Для нормальных проводников плотность тока j пропорциональна напряженности электрического поля Е: j= уЕ (у - электропроводность). Применим закон Ома (I=U/R) к однородному проводнику длиной l и сечением S. Вследствие симметрии формы провода электрическое поле в нем имеет напряженность, равную E=U/l, а плотность тока j=I/S. Подставляя эти выражения в закон Ома, получили El/Js=R, откуда j=E/с, где с-удельное сопротивление проводника, равное с=RS/l, а у=l/с – удельная электропроводность. Связь между плотностью тока и электрическим или магнитным полем для сверхпроводников дается двумя уравнениями Лондонов. Первое уравнение описывает идеальную проводимость: поле ускоряет электрон, движущийся в среде без сопротивления. Второе уравнение отражает эффект Мейснера. Оно описывает затухание магнитного поля в тонком поверхностном слое сверхпроводника и тем самым словно разрушает представление об идеальном диамагнетизме.
Диамагнетизм сверхпроводников – это поверхностный эффект, магнитное поле не проникает в толщу образца. Однако оно не может быть полностью вытолкнуто из своего объема металла, включая его поверхность. Иначе на поверхности магнитное поле скачком уменьшается до нуля. токовый слой не имел бы толщины, и плотность тока была бы бесконечной, что физически невозможно. Следовательно, магнитное поле хоть немного, проникает в проводник. Именно в этом тонком приповерхностном слое и протекают незатухающие токи, которые и экранизируют от влияния внешнего магнитного поля области, удаленные от поверхности. Толщина этого слоя, получившим название глубины проникновения поля л, является одной из важнейших характеристик сверхпроводника.