Курсовая работа: Геометрия чисел

Интересно будет кратко рассмотреть основные идеи, лежащие в основе доказательства теоремы Минковского, потому что в формальных доказательствах, приводимых основными источниками, они заслоняются необходимостью получения сильных теорем, имеющих наиболее широкие приложения.

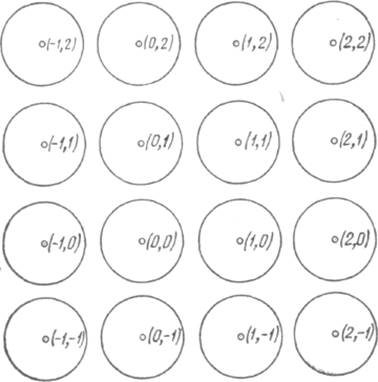
Вместо области ÂМинковский рассматривает область j = Â/2, которая состоит из точек (x₁ /2,x₂ /2), где (x₁ ,x₂ ) - точки области Â. Таким образом, область jсимметрична относительно начала координат и выпукла, её площадь равна четверти площади области Âи, следовательно, больше 1. В общем случае Минковский рассматривает совокупность областей j (u₁ ,u₂ ) сцентрами в целочисленных точках (u₁ ,u₂ ), полученных из тела j параллельными переносами.

Для начала справедливо отметить, что если j и j(u₁ ,u₂ ) пересекаются, то точка (u₁ ,u₂ ) находится в Â. Обратное утверждение тривиально. Если точка (u₁ ,u₂ ) находится в Â, то точка (u₁ /2,u₂ /2) содержится как в j, так и в j(u₁ ,u₂ ). Действительно, пусть (ξ₁ , ξ₂ ) – точка, лежащая в пересечении. Так как точка (ξ₁ , ξ₂ ) лежит в области j(u₁ ,u₂ ), то тогда точка (ξ₁ – u₁ , ξ₂ – u₂ ) лежит в области j; следовательно, ввиду симметрии области jточка (u₁ - ξ₁ , u₂ - ξ₂ ) находится в j. Наконец, в силу выпуклости тела jсередина отрезка, соединяющего точку (u₁ - ξ₁ , u₂ - ξ₂ ) с точкой (ξ₁ , ξ₂ ), то есть точка (u₁ /2,u₂ /2), лежит в j, а потому точка (u₁ ,u₂ ) находится в Â. Что, собственно, и требовалось доказать. Ясно, что область j(u₁ ,u₂ ) тогда и только тогда пересекается с областью j(u₁ ^’ ,u₂ ^’ ), когда область jпересекается с об­ластью j(u₁ - u₁ ^’ , u₂ - u₂ ^’ ).

Таким образом, чтобы теорема Минковского была доказана, достаточно показать, что если области j(u₁ ,u₂ )не пересекаются, то площадь области j(u₁ ,u₂ )не превышает 1. Небольшое размышление убеждает, что так должно быть. Другое обоснование, возможно интуитивно более ясное, можно получить, полагая, что область jцеликом содержится в квадрате

‌x₁ ‌≤ X, |x₂ | ≤ X,

при этом нужно учитывать то, что выпуклая область конечной площади ограничена.

Пусть U — достаточно большое целое число. Существует (2U + 1)² областей j(u₁ ,u₂ ), координаты центров которых удовлетворяют неравенствам

‌u₁ ‌≤ U, |u₂ | ≤ U.

Все эти области целиком находятся в квадрате

‌x₁ ‌≤ U + X, |x₂ | ≤ U + X,

площадь которого равна

4 (U + X)² .

Так как предполагается, что области j(u₁ ,u₂ ) не пересекаются, то имеет место неравенство

(2U + 1)² V £ 4(U + X)² ,

где V – площадь области j, а значит, и любой области j(u₁ ,u₂ ). Устремляя теперь U к бесконечности, мы получаем неравенство V£ 1, что и требовалось доказать.

Решётки.

Преобразование координат в приведённом примере с определённой бинарной квадратичной формой может привести и к другой точке зрения. Мы можем представить форму f(x₁ ,x₂ ) как сумму квадратов двух линейных форм

f(x₁ , x₂ ) = Х₁ ² + Х₂ ² , (3)

где

Х₁ = ax₁ + bx₂ , X₂ = gx₁ + dx₂ , (4)

a,b,g,d - некоторые постоянные вещественные числа. Можно, например, положить

a = a₁₁ ^1/2 , b = a₁₁ ^-1/2 a₁₂ ,

g = 0, d = a₁₁ ^-1/2 D^1/2 .

Обратно, если a,b,g,d - такие вещественные числа, что ab - gd¹ 0, и формы Х₁ , Х₂ заданы равенствами (4), то выражение

Х₁ ² + Х₂ ² = a₁₁ x₁ ² + 2a₁₂ x₁ x₂ + a₂₂ x₂ ² ,

где

a₁₁ = a² + g² ,

a₁₂ = ad + bg, (5)

a₂₂ = b² + d² ,

является положительно определен­ной квадратичной формой с определителем

D = a₁₁ a₂₂ – a₁₂ ² = (ad - bg)² . (6)

Теперь будем рассматривать пару (Х₁ , Х₂ )как систему пря­моугольных декартовых координат. Тогда говорят, что точки (Х₁ , Х₂ ), соответствующие целым (x₁ , x₂ ) в выражениях (4), образуют (двумерную) решетку L. В векторных обозначениях решетка L есть совокупность точек

(Х₁ , Х₂ ) = u₁ (a,g) + u₂ (b,d), (7)

где u₁ , u₂ пробегают все целые числа; точки (векторы) (a,g) и (b,d) образуют базис решётки L.

Рассмотрим теперь более подробно свойства решеток. Ввиду того, что мы рассматриваем решетку L просто как множество точек, мы можем её описать с помощью различных базисов. Например, пара

(α – β, γ – δ), (- β, - δ)

является другим базисом решётки L. Фиксированный базис (α, β), (γ, δ) решётки L определяет разбиение плоскости двумя семействами равноудалённых параллельных прямых; первое семейство состоит из тех точек (Х₁ , Х₂ ), которые имеют координаты вида (7), где u₂ – любое целое число, а u₁ – любое вещественное. Для линий второго порядка семейства u₁ и u₂ меняются ролями. Таким образом, плоскость разбивается на параллелограммы, вершинами которых являются как раз точки решётки L.

Разумеется, что это разбиение зависит от выбора базиса. Однако, можно показать, что площадь получаемых параллелограммов, именно число

|αδ – βγ|,

не зависит от выбора базиса. Это становится возможным, если показать, что число N(X) точек решётки в достаточно большом квадрате

ζ (Х): |Х₁ | ≤ Х, |Х₂ | ≤ Х

удовлетворяет соотношению

N(X) / 4X² → 1 / |αδ - βγ| (X → ∞).

Действительно, рассмотрение идей доказательства теоремы Минковского о выпуклом теле, которое было приведено в кратком виде выше, показывает, что число точек решётки L в квадрате ζ (Х), грубо говоря, равно числу параллелограммов, находящихся в этом квадрате. А это число, в свою очередь, приблизительно равно площади квадрата ζ (Х), делённой на площадь |αδ - βγ| одного параллелограмма. Строго положительное число

d (L) = |αδ - βγ| (8)

называется определителем решётки L. Как было только что показано, это число не зависит от выбора базиса.

Критические решётки.

Используя введённые выше новые понятия, можно заметить, что утверждение о существовании целых решений неравенства f(х₁ ,х₂ ) £ (4D/3)^1/2 эквивалентно утверждению о том, что любая решётка Lв области

Х₁ ² + Х₂ ² ≤ (4/3)^1/2 d(L) (9)

имеет точки, отличные от начала координат. В силу однородности это в свою очередь эквивалентно утверждению, что открытый круг

Đ: Х₁ ² + Х₂ ² < 1 (10)