Курсовая работа: Геометрия чисел

даёт информацию о минимумах inf |f(u₁ ,u₂ )| неопределённых бинарных квадратичных форм f(x₁ ,x₂ ). Здесь точная нижняя граница берётся по всем целым числам u₁ и u₂ , не равным одновременно нулю. Примеры можно продолжить.

Подобные рассмотрения приводят к следующим определениям. Говорят, что решётка L допустима для области (точечного множества) Â в плоскости {Х₁ ,Х₂ } если она не содержит никаких других точек Â, кроме, может быть, начала координат. Последний случай возможен, когда начало координат является точкой области Â. Тогда мы говорим, что эта решётка Â-допустима. Точная нижняя грань Δ(Â) определителей d(Λ) всех Â-допустимых решёток является константой области Â. Если Â-допустимых решёток не существует, то полагаем, что Δ(Â) = ∞. Тогда любая решётка Λ, для которой d(Λ) < Δ(Â), обязательно содержит точку области Â, отличную от начала координат. Â-допустимая решётка Λ, для которой d(Λ) = Δ(Â), называется критической (для Â). Конечно, критические решётки, вообще говоря, существуют не всегда.

Важность критических решёток была замечена уже Минковским. Если L_с – критическая решётка области Â, а решётка Λ получена из Λ_с небольшой деформацией (то есть малым изменением пары базисных векторов), то либо решётка Λ имеет точку, отличную от начала координат и лежащую в области Â, либо d(Λ) ≥ d(Λ_с ). Либо и то, и другое вместе.

В качестве примера можно снова рассмотреть открытый круг

Đ: Х₁ ² + Х₂ ² < 1.

Предположим, что Λ_с – критическая решётка области Đ. Ниже будет дан набросок доказательства того, что если критическая решётка существует, то она должна иметь три пары точек ±(А₁ , А₂ ), ±(В₁ , В₂ ), ±(С₁ , С₂ ) на границе Х₁ ² + Х₂ ² = 1 круга Đ.

Если Λ_с не имеет точек на окружности Х₁ ² + Х₂ ² = 1, то можно будет получить Đ-допустимую решетку с меньшим определителем, гомотетически сжимая решетку Λ_с к началу координат, то есть рассматривая решетку L = tΛ_с точек (tX₁ , tX₂ ), где (Х₁ , Х₂ ) Î Λ_с , а t — это фикси­рованное число с условием 0 < t < 1. Тогда d(L) = t² d(L_c ) < d(L_c ) и, очевидно, L будет Đ-допустимой решеткой, если t достаточно близко к 1. Таким образом, решетка L_c содержит пару точек наокружности Х₁ ² + Х₂ ² = 1, координаты которых после надлежащего поворота осей мы можем считать равными ± (1, 0).

Если бы на окружности Х₁ ² + Х₂ ² = 1 не было бы больше точек решетки L_c , то мы смогли бы получить Đ-допустимую решетку Lс меньшим определителем, сжимая решетку L_c в направлении, пер­пендикулярном оси X₁ , то есть принимая за L решетку точек (Х₁ , tХ₂ ), где (Х₁ , Х₂ ) Î Λ_с , а t достаточно близко к 1.

Наконец, если бы Λ_с имела бы только две пары точек ±(1, 0), ± (В₁ , В₂ ) на границе, то решетку можно было бы слегка деформиро­вать так, чтобы точка (1, 0) осталась на месте, а точка с координатами (В₁ , В₂ ) продви­нулась бы вдоль окружности Х₁ ² + Х₂ ² = 1 ближе к оси Х₁ . Наглядно это представлено на рисунке:

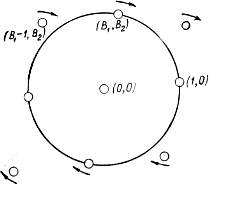
Данная операция, как легко проверить, уменьшает определитель, и при небольших деформациях получающаяся решётка Λ остаётся Đ-допустимой. Действительно, (1,0) и (В₁ , В₂ ) можно рассматривать как базис решётки Λ_с , так как треугольник с вершинами (0, 0), (1, 0), (В₁ , В₂ ), а следовательно, и параллелограмм, отвечающий базису (1, 0), (В₁ , В₂ ) не содержит внутри себя точек Λ_с . Тогда критическая решётка Λ_с (если она существует) должна иметь три пары точек на окружности Х₁ ² + Х₂ ² = 1. Легко увидеть, что единственной решеткой, у которой три пары точек лежат на окружности Х₁ ² + Х₂ ² = 1, а одна из пар есть пара ± (1, 0), является решетка Λ ́ с базисом

(1, 0), (1/2, √3/4).

Она содержит вершины правильного шестиугольника

± (1, 0), ± (1/2, √3/4), ±(-1/2, √3/4),

лежащие на окружности Х₁ ² + Х₂ ² = 1, но не содержит ни одной точки (кроме (0, 0)) в круге Х₁ ² + Х₂ ² < 1. Таким образом, мы по­казали, что если Đ имеет критическую решетку, то Δ(Đ) = d(Λ ́) = (3/4)^1/2 . Минковский показал, что критические решетки существуют для довольно широкого класса областей Â, показав, грубо говоря, что любую Â-допустимую решетку Λ можно постепенно деформи­ровать до тех пор, пока она не станет критической.

“Неоднородная задача”

Другим общим типом проблемы является следующая типичная «неоднородная задача». Пусть f(х₁ ,…,x_n )— некоторая вещественнозначная функция вещественных аргументов х₁ , . . ., х_n . Требуется подобрать постоянное число k со следующим свойством: если ξ₁ , ...,ξ_n — любые вещественные числа, то найдутся такие целые числа u₁ ,…,u_n , что

│f(ξ₁ – u₁ ,…, ξ_n – u_n )│≤ k.

Подобные вопросы естественно возникают, например, в теории алгебраических чисел. И на этот раз имеется простая геометрическая интерпретация. Для наглядности положим n = 2.Пусть Â — мно­жество таких точек (х₁ ,х₂ ) двумерной евклидовой плоскости, что

│f(x₁ , …, x_n )│≤ k.

Пусть u₁ , u₂ — любые целые числа; обозначим через Â(u₁ , u₂ ) об­ласть, полученную из Â параллельным переносом на вектор (u₁ , u₂ ); иными словами, Â(u₁ , u₂ ) есть множество таких точек х₁ ,х₂ , что

│f(х₁ – u₁ , х₂ – u₂ )│≤ k.

Неоднородная проблема состоит в выборе k таким образом, чтобы области Â(u₁ , u₂ ) покрывали всю плоскость. Желательно выбрать k, а значит и Â, наименьшим из всех возможных (но так, чтобы свой­ство покрывать всю плоскость сохранилось). Здесь мы имеем про­тивоположность постановке однородной задачи, приведённой выше, где цель состояла в том, чтобы сделать области наибольшими, но все еще не пересекающимися одна с другой.

Список литературы.

1. Касселс, Дж. В. С. Геометрия чисел – М., Мир, 1965г.

2. Минковский Г. Геометрия чисел – Лейпциг, 1911г. (переиздание 1996г.)

3. Марков А. А. О бинарных квадратичных формах положительного определителя – СПб., 1948г.

4. Чеботарёв М. Г. Заметки по алгебре и теории чисел – УЧ Зап. Каз. Унив-та, 1934г. (переиздание 1994г.)

5. Чеботарёв М. Г. Доказательство теоремы Минковского о неоднородных линейных формах – М., Мир, 1949г.