Курсовая работа: Гидравлика

- кинематический коэффициент вязкости жидкости.

Экспериментально определено, что режим будет ламинарным, если .

- критическое число Рейнольдса, при котором происходит переход ламинарного режима в турбулентный. Для круглых труб принимают. Если число Рейнольдса находится в области , то режим считается переходным, а при - турбулентным.

Ламинарный режим возникает в тонких капиллярных трубках, во время движения очень вязких жидкостей, при фильтрации воды в слоях грунта и др. Движение маловязких жидкостей (вода, бензин, спирт) почти всегда происходит в турбулентном режиме.

4 Гидравлические сопротивления

4.1 Общие сведения о гидравлических потерях

Движение вязкой жидкости сопровождается потерями энергии.

Потери удельной энергии (напора), или гидравлические потери, зависят от формы, размеров русла, скорости течения и вязкости жидкости.

В большинстве случаев гидравлические потери пропорциональны скорости течения жидкости во второй степени или динамическому напору и определяются из выражения

(4.1)

где - коэффициент потерь; V-средняя скорость в сечении.

Потери в единицах давления

. (4.2)

Гидравлические потери энергии обычно разделяют на местные потери и потери на трение по длине

. (4.3)

Местные потери энергии обусловлены так называемыми местными гидравлическими сопротивлениями, т.е. местными изменениями формы и размеров русла, вызывающими деформацию потока. При протекании жидкости через местные сопротивления изменяется ее скорость и возникают вихри.

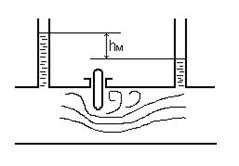
Примером местных сопротивлений может служить задвижка (рис.4.1).

Рисунок 4.1 – Местное гидравлическое сопротивление: а) задвижка

Местные потери напора определяются по формуле Вейсбаха

, (4.4)

где V-средняя скорость в трубе;-коэффициент местного сопротивления.

Потери на трение по длине -это потери энергии, которые возникают в прямых трубах постоянного сечения и возрастают прямо пропорционально длине трубы (рис.4.2).

Рассматриваемые потери обусловлены внутренним трением жидкости в трубах. Потери напора при трении определяются по формуле Дарси-Вейсбаха

, (4.5)

где λ – коэффициент гидравлического трения по длине или коэффициент Дарси; l – длина трубопровода; d –его диаметр; V – средняя скорость течения жидкости.

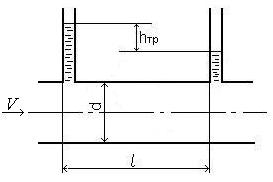Рисунок 4.2 – Потери напора по длине трубы

Для ламинарного режима движения жидкости в круглой трубе коэффициент определяется по теоретической формуле

, (4.6)

где число Рейнольдса.

При турбулентном режиме коэффициент зависит от числа Рейнольдса Reи относительной шероховатости(-эквивалентная шероховатость) и определяется по эмпирическим формулам.

В области гидравлически гладких труб 4000<Re<, т.е. при малых скоростях и числах Рейнольдса, коэффициент Дарси зависит только от числа Рейнольдса, и его определяют по формуле Блазиуса