Курсовая работа: Групповая работа на уроках математики в начальной школе
Величина, так же как и число, является основным понятием курса математики начальных классов, в задачу которого входит формирование у детей представления о величине как о некотором свойстве предметов и явлений, которое прежде всего связано с измерением.
В 1-3 классах учащиеся получают представление о таких величинах, как длина, масса, емкость, время, площадь, и о единицах ее измерения. В процессе решения задач они знакомятся с ценой, количеством, стоимостью, скоростью, расстоянием, производительностью и т.д.
В процессе изучения темы важно добиться, чтобы учащиеся научились четко дифференцировать такие тесно связанные между собой, но разные по своей сути понятия, как "величина" и "число". Хотя формирование представлений о той или иной конкретной величине и о способах ее измерения имеет свои особенности, тем не менее, целесообразно выделить общие этапы, которые имеют место при изучении каждой из величин:
1. Выяснение и уточнение имеющихся у детей представлений о данной величине (обращение к опыту ребенка).
2. Сравнение однородных величин (визуально, с помощью ощущений, наложением, приложением, путем использования различных мерок).
3. Знакомство с единицей измерения данной величины и с измерительным прибором.
4. Формирование измерительных умений и навыков.
5. Сложение и вычитание однородных величин, выраженных в единицах одного наименования.
6. Знакомство с новыми единицами величины, перевод однородных величин, выраженных в единицах одних наименований, в другие, перевод величин, выраженных в единицах одного наименования, в величины, выраженные в единицах двух наименований, и наоборот.
7. Сложение и вычитание величин, выраженных в единицах двух наименований.
8. Умножение и деление величины на число.
С целью формирования представлений о разного рода величинах проводятся практические работы, используются упражнения, применяются демонстрационные и индивидуальные наглядные средства, при этом варьируются коллективные, индивидуальные и групповые формы работы на уроке.
Значение с величинами единицами их измерения имеет не только практическое значение: оно предоставляет большие возможности для формирования умения видеть проблему и находить пути ее решения, тем самым способствуя развитию познавательных способностей учащихся.
1.3 Общая характеристика методики изучения площади младшими школьниками
Методика формирования представлений о площади фигуры строится в соответствии с общей методикой формирования представлений о величинах. При этом изучение понятия площади проводится с опорой на привычные для детей представления о том, что каждая фигура занимает определенное - большее или меньшее – место на плоскости.
Для разъяснения понятия используются демонстрационные или индивидуальные модели различных фигур (рис.1).
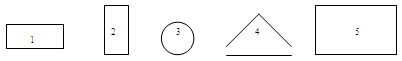
Рисунок 1.
Путем наложения их друг на друга учащиеся устанавливают, что площади первой и второй фигур одинаковы, а площадь четвертой меньше площади пятой, так как вся четвертая фигура помещается внутри пятой, и т.д. учитель может предложить выписать номера фигур, расположив их в порядке возрастания площадей. в процессе таких упражнений уточняются представления детей о площади.
После этого учитель может раздать ученикам листы клетчатой бумаги, на которой изображены различные фигуры и предложить сравнить площади этих фигур. Учащиеся сами догадываются, что для этого нужно сосчитать число клеток в каждой фигуре. Фигура, содержащая большее число клеток, имеет большую площадь.
Такого рода задания подводят учащихся к осознанию необходимости введения общепринятой единицы площади 1 см2 . (квадрат со стороной, равной одному сантиметру). У каждого ученика должна быть модель квадратного сантиметра.
Для того чтобы учащиеся освоили процесс измерения площади полезно раздать им геометрические фигуры и предложить им измерить их площади, пользуясь моделью квадратного сантиметра. Это задание особенно важно, так как в процессе его выполнения учащиеся осознают, что измерить площадь фигуры – значит узнать, сколько квадратных сантиметров она содержит. Учащиеся практически убеждаются, что укладывать модель квадратного сантиметра в фигуре долго и неудобно – гораздо удобнее использовать прозрачную бумагу, на которой нанесена сетка из квадратных сантиметров. Таким образом, учащиеся знакомятся с палеткой и правилами пользования ею, упражняются в определении площадей фигур с ее помощью.
При определении площади прямоугольника необходимо также широко использовать практический метод. Это поможет учащимся осознать тот факт, что найти площадь прямоугольника – значит узнать, сколько квадратных сантиметров в нем содержится.
Глава II . Методика изучения площади геометрических фигур и единиц ее измерения на уроках математики в начальной школе
2.1 Методика обучения измерению величин
В начальных классах рассматриваются величины: длина, площадь, масса, емкость, время и др. учащиеся должны получить конкретные представления об этих величинах, ознакомиться с единицами их измерения, овладеть умениями измерять величины, научиться выражать результаты измерения в различных единицах, выполнять арифметические действия над величинами.
Изучение величин имеет большое значение, так как понятие величины является важнейшим понятием математики. Каждая изучаемая величина – это некоторое обобщенное свойство реальных объектов окружающего мира. Упражнения в измерениях развивают пространственные представления, вооружают учащихся важными практическими навыками, которые широко применяются в жизни. Следовательно, изучение величин – это одно из средств связи обучения с жизнью.
Длина отрезка. Первые представления о длине как свойстве предметов у детей возникают задолго до школы. К началу обучения в школе дети правильно устанавливают отношения: длиннее – короче, шире – уже, дальше – ближе и т.п., если различия в этом плане ярко выражены, а по другим свойствам предметы сходны.
С первых дней обучения в школе ставится задача уточнять пространственные представления детей. Этому помогают упражнения на сравнение предметов по протяженности, например: "Какая книга тоньше (книги прикладываются друг к другу)? Кто ниже: Саша или Оля (дети ставятся рядом)? Что глубже: ручей или река (по представлению)? В процессе этих упражнений отрабатывается умение сравнивать предметы по длине, а также обобщается свойство, по которому происходит сравнение – линейная протяженность, длина.