Курсовая работа: Игра в "Морской бой" с компьютером
На этом этапе компьютер должен поймать какой-либо из кораблей противника. Для этого он будет стрелять по произвольным незанятым клеткам поля игрока. Гораздо эффективнее сначала разделаться с большими кораблями, поэтому выбирая координаты для выстрела надо проверять, что бы в этой позиции мог разместиться самый большой из оставшихся кораблей. Процесс прекращается, как только произойдет попадание. Обозначим подбитую часть корабля значением «*», а промах «~» соответствующей ячейки поля. Если у игрока остались только однопалубные корабли, то этим попаданием корабль уничтожен полностью и обстреливать его нет смысла. В противном случае надо перейти ко второму состоянию.
Обстрел
На этом шаге задача заключается в определении направления пойманного корабля. Для этого надо обстрелять четыре ячейки (если они свободны), которые могут служить продолжением. В случае, когда все четыре клетки обстреляны, а попадания не произошло (однопалубный корабль), надо перейти к первому состоянию. Если в какой-то момент удалось подбить еще одну палубу противника, то можно переходит к расстрелу данного корабля, т. к. его направление стало известно. Аналогично первому состоянию, если у игрока остались корабли не более двух палуб, то этим попаданием корабль уничтожен полностью и надо вернуться к прострелу.
Расстрел
На предыдущем шаге удалось установить в каком направлении размещен пойманный корабль. Теперь задача заключается в его полном уничтожении. Для этого надо стрелять справа или слева (сверху или снизу) подбитых палуб, пока не добьем его целиком, после чего вернемся в состояние прострела. При этом следует учитывать максимально возможный корабль и стараться попасть по четвертой палубе, когда четырех палубный корабль уничтожен, нет никакого смысла.
Пример
Поле кораблей
| 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
Стратегия игры компьютера.
1. Выбирается случайная клетка, рассматривается ее значение.
2. Если значение = 1 – попали в корабль, отмечаем удар «*»;
3. Если значение = 0 – промазали, отмечаем удар «~»;
4. Если значение = «*» или значение = «~», значит в эту клетку нами уже был произведен удар, возвращаемся к шагу 1.
После того как все корабли разбиты, прекращаем бой. Поле разбитых кораблей
| * | * | * | * | ~ | ~ | * | ~ | ~ | ~ |
| ~ | ~ | ~ | ~ | ~ | ~ | * | ~ | ~ | ~ |
| ~ | ~ | ~ | ~ | * | ~ | * | ~ | ~ | ~ |
| * | ~ | ~ | ~ | * | ~ | ~ | ~ | ~ | ~ |
| ~ | ~ | ~ | ~ | ~ | ~ | ~ | ~ | ~ | ~ |
| ~ | ~ | ~ | ~ | 0 | ~ | ~ | ~ | ~ | ~ |
| ~ | ~ | * | ~ | ~ | ~ | ~ | ~ | 0 | * |
| ~ | ~ | ~ | ~ | ~ | ~ | ~ | ~ | ~ | * |
| ~ | ~ | ~ | ~ | * | * | ~ | ~ | ~ | ~ |
| * | ~ | * | ~ | ~ | ~ | ~ | * | * | * |
Нулями обозначены те клетки, в которые мы не попали.
2. Математические и алгоритмические основы решения задачи
Для того чтобы приступить к построению и анализу математической модели игры, необходимо определить вероятности обнаружения кораблей при различном их расположении и различных системах поиска
На поле из n клеток расположен одноклеточный корабль. Определим вероятность попадания в корабль k-ым выстрелом, то есть его уничтожение.
В качестве пространства элементарных исходов выбора игрока В рассмотрим множество стратегий обстрела игрового поля, каждая стратегия состоит из n выстрелов,
![]() ,
,
где ![]() – номер выбранной клетки, то есть рассмотрим множество всех выборок из n по n клеток. Очевидно, что это пространство содержит
– номер выбранной клетки, то есть рассмотрим множество всех выборок из n по n клеток. Очевидно, что это пространство содержит ![]() элементов и все эти стратегии равновозможны. Количество стратегий с благоприятным исходом, то есть количество выборок, содержащих на k-ом месте искомую клетку
элементов и все эти стратегии равновозможны. Количество стратегий с благоприятным исходом, то есть количество выборок, содержащих на k-ом месте искомую клетку
![]() .
.
Вероятность попадания
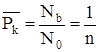 .
.
Определим вероятность уничтожения корабля за k выстрелов. Это событие состоит в том, что корабль может быть уничтожен либо первым выстрелом, либо вторым и т.д., то есть благоприятная выборка из k клеток содержит искомую клетку с кораблем. Количество благоприятных стратегий определится как число неупорядоченных выборок из множества n – 1 клеток по k – 1 (одна клетка, занятая кораблем не учитывается при выборке), умноженное на число перестановок в самой выборке k! и число перестановок клеток оставшихся за выборкой (n – k)!:)!. Вероятность попадания в одноклеточный корабль за k выстрелов
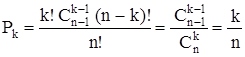 . (1)
. (1)
Усложним задачу. На поле из n клеток расположен двухклеточный корабль. Определим вероятность первого попадания в корабль (в одну из его клеток) выстрелом с номером k. Полное число всевозможных стратегий, как и в предыдущем случае, равно ![]() , а число благоприятных стратегий определяется как сумма благоприятных стратегий попадания в одну клетку и попадания во вторую клетку, то есть
, а число благоприятных стратегий определяется как сумма благоприятных стратегий попадания в одну клетку и попадания во вторую клетку, то есть ![]() . Вероятность попадания k-ым выстрелом равна
. Вероятность попадания k-ым выстрелом равна ![]() .
.
Очевидно, что при обстреле m-клеточного корабля или m одноклеточных кораблей, вероятность попадания k-ым выстрелом равна
![]() .
.
Определение вероятности попадания в двухклеточный корабль за k выстрелов, сведется к определению количества стратегий, содержащих искомые клетки в первых k выстрелах. Число таких стратегий будет вычисляться как следующая сумма