Курсовая работа: Информатика Алгоритмизация и программирование
2. Интеграл представляет собой площадь криволинейной трапеции, ограниченной осью OX, прямыми x=aи x=bи графиком функции. Очевидно, что интеграл от функции на отрезке равен сумме интегралов от этой же функции на каждом из маленьких отрезков, полученных в результате разбиения. Но на каждом из маленьких отрезков мы приближенно заменяем площадь криволинейной трапеции на площадь прямолинейной трапеции с основанием (высотой), равным длине маленького отрезка, и высотами (основаниями) f(xn ) и f(xn +1 ), где xn – левая граница отрезка, xn +1 – правая граница отрезка. Основание (высота трапеции) равно
(b-a)/n, и таким образом площадь трапеции равна
(f(xn )+f(xn +1 ))(b-a)/2n. У нас всего n трапеций, причем каждые две соседние трапеции имеют одинаковые высоты (основания). Таким образом, в сумму каждое из f(xn ) кроме f(a) и f(b) войдет дважды, и таким образом весь интеграл вычисляется как 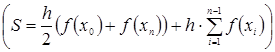 , где
, где ![]() .
.
3. В методе трапеций не определен шаг (количество отрезков разбиения). Очевидно, что чем больше количество отрезков, тем более точным будет результат. Поэтому, задаем начальное значение n (например n=10) и вычисляем интеграл.
4. После этого удваиваем n и снова вычисляем интеграл (п. 2). Сравнивая полученные результаты, делаем вывод, достигнута ли требуемая точность.
5. Если результаты отличаются друг от друга меньше чем на ε, то требуемая точность достигнута. Если нет, то снова удваиваем n и вычисляем интеграл еще раз (возвращаемся к п. 4).
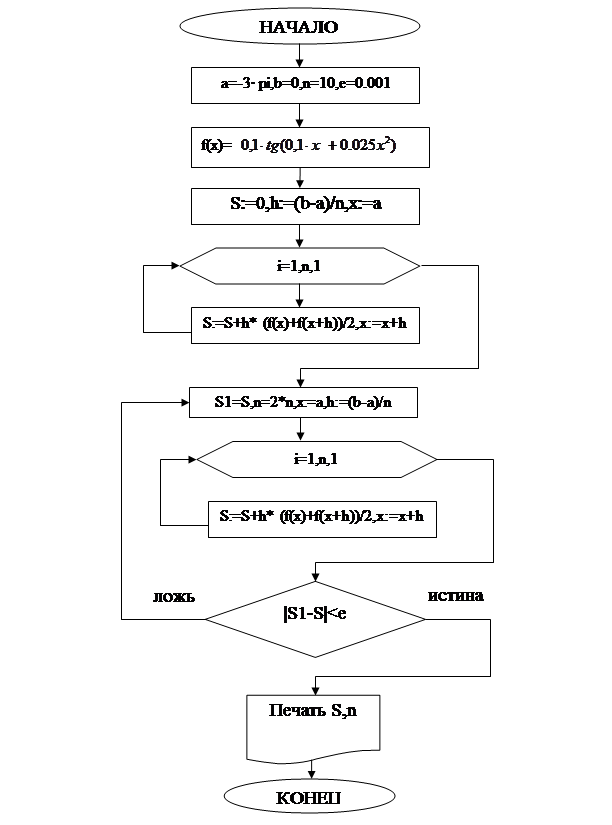
Ниже представлена блок-схема алгоритма и листинг программы.
program pr4;
uses crt;
var
h,a,b,S,dS,P,x,eps:real;
n,i:integer;
function f(x:real) : real;
begin
f:=0,1*sin(0.1*x+0.0025*x*x)/cos(0.1*x+0.0025*x*x);
end;
begin
clrscr;
writeln('input a,b,n,eps, please');
write('a');
readln(a);
write('b');
readln(b);
write('n');
readln(n);
write('eps');
readln(eps);
s:=0;
repeat P:=S;
h:=(b-a)/2;