Курсовая работа: IP-телефония и видеосвязь
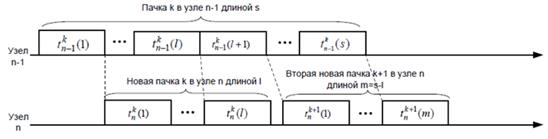
Рисунок 1.3.3 - Фрагментация пачки k в узле n
Математический анализ этих двух явлений эффекта туннелирования MPLS позволяет вывести следующую формулу для времени пребывания пакета в туннеле из N узлов:
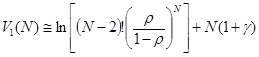 (1.3.1)
(1.3.1)
где γ- постоянная Эйлера (γ≈0.577 ), N > 2.
Формула (1.3.1) позволяет рассчитать целесообразность организации туннеля в LSP для индивидуальных пар «исходящий узел - узел назначения» при заданных загрузке сети р и нормативах качества обслуживания. С ее помощью дается можно показать, что отдельные туннелированные LSP в наиболее реалистических случаях, вероятно, должны являться предпочтительным режимом работы.
Рассмотрим маршрут в MPLS - сети, который состоит из N узлов и физических каналов передачи данных между ними. Маршрут соответствует трем объектам: LSRH (LSR источника), LSRн (LSR назначения) и классом обслуживания трафика, передачи.
Пусть λ-прежнему означает число запросов, а 1/μ означает усредненное время определяемым допустимым временем интенсивности пуассоновского потока обслуживания сообщений в узле. Соответственно, ρ=λ/μ означает нагрузку, обслуживаемую узлом LSP- маршрута. Обслуживание же этой нагрузки узлами, входящими в данный LSP- маршрут, и является основной работой данного фрагмента сети MPLS.
В контексте поставленной задачи поиска стратегии принятия решения об организации LSP- туннеля для оценки альтернативного варианта суммарного времени V2 (N) пребывания пакета в LSP- пути без туннеля допустимо использовать В-формулу Эрланга в качестве адекватной оценки, позволяющей произвести сравнение с V1 (N).
На рисунке 1.3.4 представлены оба варианта передачи сообщений при наличии или при отсутствии LSP- туннеля. В первом случае суммарное время пребывания пакета в сети равно V1 (N), а во втором случае время пребывания того же пакета в сети равно V2 (N). Для аналитического исследования ситуации отсутствия LSP- туннеля узел п, передающий пакеты по LSP, целесообразно описать с помощью модели М/М/1/К со скоростью передачи
μ2 =μ/(1+μ)
пакетов в секунду и максимальным числом к пакетов, и которое он может хранить в своей буферной памяти. Пакеты в этой модели являются теми же самыми, что в случае организации туннеля, а ограничение на размер буфера выбрано так, чтобы условия в вариантах наличия или отсутствия туннеля были бы абсолютно одинаковы.
Инженерные различия между MPLS и традиционным туннелированием состоит в модели топологии MPLS. Традиционные туннели всегда проходят от одной границы до другой насквозь через сеть. В случае MPLS туннели могут создаваться внутри сети для управления трафиком только в части сети .т.е в LSP из М маршрутизаторов от входящего LSRi до исходящего LSRm можно создать LSP-туннель, например, от входящего LSRs до исходящего LSRn , при N<M. Т.е. даже создаваемые на короткое время LSP - туннели в MPLS могут начинаться внутри сети, а не из пользовательского приложения" па границе сети. Это особенно важно для практического применения представленной модели: пользователи будут продолжать применять обычные IP- пакеты и адресацию в своих приложениях и даже в локальных сетях. Эффект от организации туннеля, равен разности V1 и V2. При этих предположениях предлагается следующий алгоритм:
Шаг 1. Полагается N = М.
Шаг 2. Для п = 1,2 N определяются величины размера пачки в Кn по формуле
![]() (1.3.2)
(1.3.2)
Шаг 3. Определяется время V2 (N) пребывания пакета в LSP - пути сети MPLS из N узлов (маршрутизаторов) без организации LSP - туннеля при наличии ограниченной очереди к узлу n длиной Кn по формуле