Курсовая работа: Использование математических методов и моделей в управлении микроэкономическими системами
6
1-2-3-4-5-6 или 1-4-5-6
22
7
1-2-3-4-5-6-7 или 1-4-5-6-7
25
Пример:
Транспортная компания выбирает маршрут из пункта 1 в пункт 7 для доставки товара и желает сократить время в пути своего автотранспорта. Время необходимое для перевозки товара по каждому участку пути обозначено рядом с каждым ребром сети. Необходимо проложить маршрут, обеспечивающий минимальное время автотранспорта в пути.
С помощью алгоритма построения кратчайшего маршрута такой тип задачи можно решить. В результате расчетов минимальное время в пути будет составлять 25 часов.
4. Нахождение максимального потока.
Найти максимальный поток можно одним из нижеописанных способов.
4.1 Серия последовательных шагов.
На графиках укажем степень насыщения потока над каждым ребром, а в скобках остаточную пропускную способность.
Шаг 1: построим поток 1-2-3-4-5-6-7 и найдем максимальную пропускную способность этого пути.
Min ( Cij ) = C 34 = 2
Φ 1 = 2
Поток не полный
Шаг 2: построим поток 1-4-5-6-7
Min ( Cij ) = C 45 = 1
Φ 2 = Φ 1 + 1= 3
 |
Поток не полный
Шаг 3: построим поток 1-4-7
Min ( Cij ) = C 14 = 10
Φ 3 = Φ 2 + 10= 13
Φ 3 =13 – полный поток
4.2 Метод разделяющих сечений
Обозначим все возможные разделяющие сечения данной сети и опишем их характеристики ниже.
 |
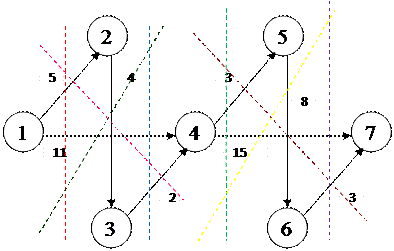1) 
Χ = {1}, 
= {2, 3, 4, 5, 6, 7}
С1 = С(1; 2) + С(1; 3) = 5+11=16