Курсовая работа: Исследование арифметико–логического устройства для выполнения логических операций

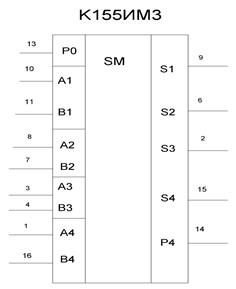
Рисунок 4 – Двоичный сумматор К555ИМ3

13-ввход переноса; 10,11,8,7,3,4,1,16-входы ;12-общий; 9,6, 2, 15-выходы суммы; 5-UЛ выход переноса.

Необходимо спроектировать сумматор, который имеет модель типа К555ИМ3. Для того чтобы узнать сигналы на выходе четырехразрядного сумматора К555ИМ3 при подаче на входы сигналов 0100 и 1101, необходимо сложить эти числа.

С = 0011 - первое слагаемое

+

D = 1100 - второе слагаемое

_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _

С+D = 01111 - сумма

Таблица 1 – сигналы на сумматоре поле выполнения операции

Сумма этих чисел и будет на выходе сумматора. Сигналы на входе и выходе сумматора показаны на рисунке 5

DD2	A4	0	P4	0
	B4	1
	A3	1	S4	1
	B3	1
	A2	1	S3	1
	B2	1
	A1	0	S2	1
	B1	1
	P0	0	S1	1

Для построение 8 разрядного сумматора необходимо соединить 2 четырехразрядных сумматора К555ИМ3, способом, показанным на рисунке 5

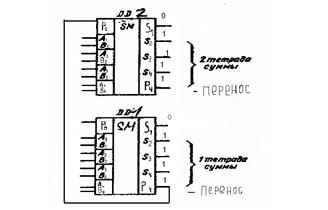
Рисунок 5 – Способ построения 8 разрядного сумматора на базе двух четырехразрядных сумматора К555ИМ3

При построении сумматора для восьмиразрядных чисел нужно учитывать, что на входы этого сумматора слагаемые поступают параллельно, а перенос между разрядами передается последовательно.

Для расчета сигналов на выходе восьмиразрядного сумматора при подаче на вход сигналов 11110000 и,00000001 необходимо сложить эти числа.

Выполним сложение двух восьмиразрядных чисел С и D.

С = 1111 0000 - первое слагаемое

+

D = 0000 001 - второе слагаемое

_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _

С+D = 01111 0001 - сумма

2 тетрада 1 тетрада

1 тетрада – 4 младших разряда числа

2 тетрада – 4 старших разряда числа

Для сложения старшие разряды чисел С и D поступают на информационные входы микросхемы DD2, а цифры младших разрядов – на входы DD1 параллельным способом. Сигналы на выходах и входах микросхему после выполнения операции показаны на таблице 2

Таблица 2 – Значения сигналов на выходах и входах микросхему К555ИМ3 после выполнения сложения 11110000 и 00000001.

DD2	A4	0	P4	0
	B4	1
	A3	0	S4	1
	B3	1
	A2	1	S3	1
	B2	0
	A1	1	S2	1
	B1	0
	P0	1	S1	1
DD1	A4	0	P4	0
	B4	1
	A3	0	S4	0
	B3	1
	A2	1	S3	0
	B2	0
	A1	1	S2	0
	B1	0
	P0	0	S1	1

Выполним перевод результата сложения из двоичной системы счисления в десятичную, восьмеричную и шестнадцатеричную системы счисления. Для удобства сначала переведем число в шестнадцатеричную систему счисления, затем в десятичную и восьмеричную системы счисления.

Для перевода двоичного числа в шестнадцатеричную систему счисления необходимо разложить число на тетрады и перевести его в шестнадцатеричную систему счисления, затем сложить их согласно приоритету тетрада.