Курсовая работа: Исследование индуцированной шумом синхронизации в системах с дискретным временем
Значение управляющего параметра ![]() ,
, ![]() - параметр связи
- параметр связи
Случайная величина ![]() подчиняется нормальному распределению
подчиняется нормальному распределению 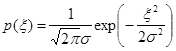 , где,
, где,![]() .
.
Бифуркационная диаграмма для данного отображения имеет вид:
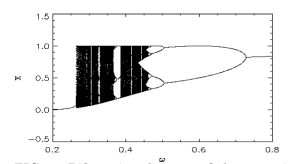
Результаты, полученные с помощью созданной программы
1. Для отображения ![]() , где
, где ![]() при
при ![]()
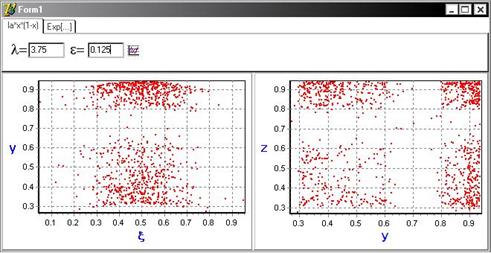
Видно, что в случае малого параметра связи (![]() ) обе системы в один момент дискретного времени принимают разные значения (точки, характеризующие состояние систем, распределены по плоскости (y,z)), а следовательно не существует функциональной зависимости между случайным процессом и состоянием динамической системы.
) обе системы в один момент дискретного времени принимают разные значения (точки, характеризующие состояние систем, распределены по плоскости (y,z)), а следовательно не существует функциональной зависимости между случайным процессом и состоянием динамической системы.
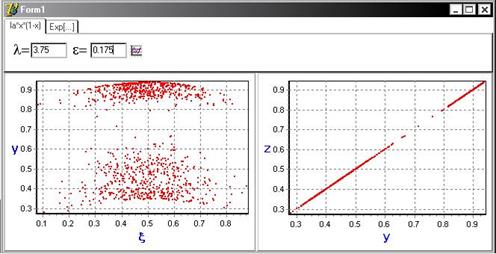
С увеличением параметра связи ![]() : точки соответствующие состояниям систем, лежаться на диагональ y=z, что свидетельствует о наличии синхронного поведения в системе.
: точки соответствующие состояниям систем, лежаться на диагональ y=z, что свидетельствует о наличии синхронного поведения в системе.
3. Для отображения ![]() , где
, где 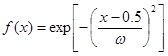 , при
, при ![]() получаем аналогичные результаты: при
получаем аналогичные результаты: при ![]() синхронизации не наблюдается:
синхронизации не наблюдается:
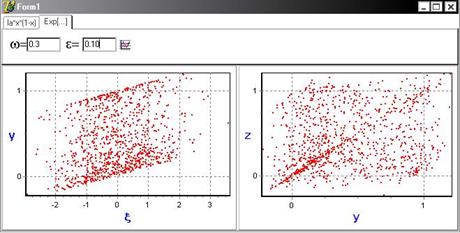
Но с увеличением параметра связи ε=0.2 появляется функциональная зависимость, что свидетельствует об установлении режима индуцированной шумом синхронизации.
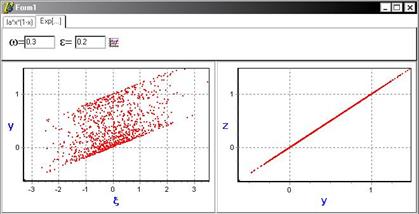
С помощью данной программы было найдено, что порог синхронизации индуцированной шумом:
-для первого отображения ![]()
-для второго отображения ![]()
Ляпуновские экспоненты
Как уже было упомянуто ранее, установление синхронной динамики двух систем с общим источником шума возможно лишь в том случае, когда ляпуновские экспоненты оказываются отрицательными.
Для отображений ляпуновский показатель рассчитывается по формуле:
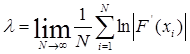 [5] ,
[5] ,
где F(x) – функция, задающая отображение.
Для рассматриваемых систем зависимость ляпуновской экспоненты от управляющего параметра ![]() имеет вид:
имеет вид:
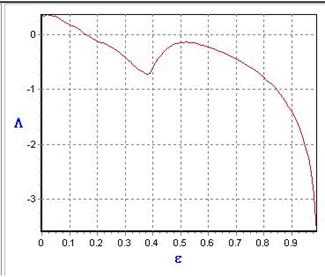
1. ![]() , где
, где ![]()
2. ![]() , где
, где 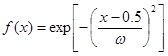
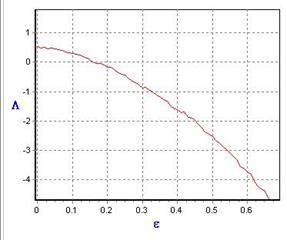
Видно, что для логистического отображения (1) ляпуновская экспонента становится отрицательной при e = 1.165, для отображения (2) – при e = 1.151.Таким образом, результаты, полученные при помощи обоих методов диагностики, оказываются приблизительно одинаковыми.
Выводы