Курсовая работа: Исследование модели электролитического осаждения меди

a) найдем ток, протекающий через установку:

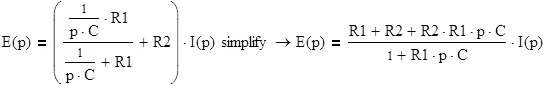б) найдем количество меди и передаточную функцию:

в) построим физико-математическую модель:

4 Определение характеристик

а) зависимость тока от времени, используя преобразование Лапласа

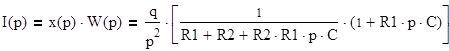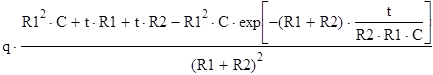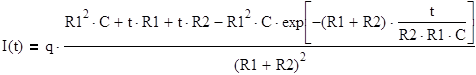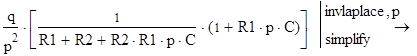
б) частотные характеристики ТС

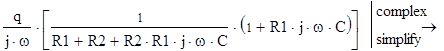
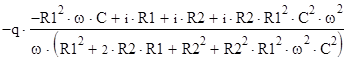действительная часть:

мнимая часть:

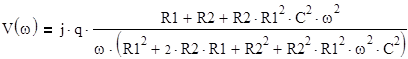5 Общие нелинейные дифференциальные уравнения

Пусть u= u( x₁ , x₂ ,…, x_n ) – функция, определенная в любой точке действительных чисел. Градиентом u является N - вектор-функция, обозначаемая gradu и определенная следующим образом:

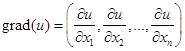(1)

В дальнейшем будем прежде всего иметь дело с функциями, определенны­ми в плоских областях, т.е. при N = 2. Для функции u = u (х, у) имеем

(2)

5.1 Нелинейный оператор Лапласа

Рассмотрим плоскую область и функцию и =и(х,у), удовлетворяющую уравнению

(3)

где f = f(х,у ) - заданная на функция, а р - действительное число, удовлетворяющее условию р > 1.

Мы не знаем, имеет ли уравнение (3) какой-либо физический смысл. Тем не менее оно полезно с методологической точки зрения и мы будем часто им пользоваться, чтобы проиллюстрировать различные понятия и утверждения. Так как при р = 2 левая часть уравнения (3) представляет собой оператор Лапласа, а само уравнение (3) сводится к уравнению Пуассона, то можно называть

(4)

выражение нелинейным оператором Лапласа.

5.2 Уравнение Монжа—Ампера