Курсовая работа: Исследование операций и Теория систем 3

Авиакомпания обслуживает два города. Первому городу требуется тоннаж в С₁ , а второму – в С₂ т. Избыточный тоннаж не оплачивается. Каждый самолет в течение дня может выполнить только один рейс.

Расходы, связанные с перелетом самолетов по маршруту «центральный аэродром – пункт назначения», обозначены символом a_ij , где первый индекс соответствует номеру города, а второй – типу самолета.

А₁ =8, А₂ = 15, А₃ =12, В₁ = 45, В₂ = 7, В₃ = 4, С₁ = 20000, С₂ = 30000, a₁₁ = 23,
a₁₂ = 5, a₁₃ = 1.4, a₂₁ = 58, a₂₂ = 10, a₂₃ =3.8.

Решение

1. Составим математическую модель задачи. Возьмём в качестве целевой функции расходы на перелеты самолетов (соответственно, необходима минимизация целевой вункции), а в качестве переменных – число рейсов в день x_ij , где первый индекс соответствует номеру города, а второй – типу самолета.

Целевая функция:

Ограничений задачи:

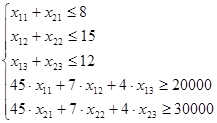
Основная задача линейного программирования:

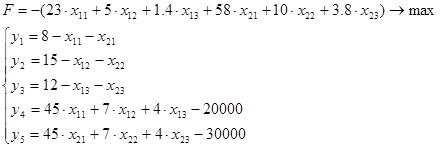
2. Правую часть уравнений (ограничения и целевую функцию) представляем в виде разности между свободным членом и суммой всех остальных:

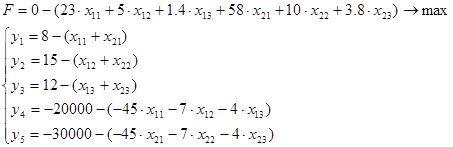
Составим симплекс – таблицу:

bi		x11		x12		x13		x21				x22				x23
0	23	5	7/5	58		10		19/5
y1	8	1	0	0	1		0		0
	y2	15	0	1	0	0		1		0
y3		12	0	0	1	0		0		1
	y4	-20000	-45	-7	-4	0		0		0
y5		-30000	0	0	0	-45		-7		-4
	bi		x11		x12		x13		x21			x22				x23
0	23	5	7/5	58	10		19/5
-150	0	-10	0	0		-10		0
y1	8	1	0	0	1	0		0
	0	0	0	0	0		0		0
y2	15	0	1	0	0	1		0
	15	0	1	0	0		1		0
y3	12	0	0	1	0	0		1
	0	0	0	0	0		0		0
y4	-20000	-45	-7	-4	0	0		0
	0	0	0	0	0		0		0
y5	-30000	0	0	0	-45	-7		-4
	105	0	7	0	0		7		0

bi		x11		x12		x13		x21		y2		x23
-150	23	-5	7/5	58	-10	19/5
-228/5	0	0	-19/5	0	0	-19/5
y1	8	1	0	0	1	0	0
	0	0	0	0	0	0	0
x22	15	0	1	0	0	1	0
	0	0	0	0	0	0	0
y3	12	0	0	1	0	0	1
	12	0	0	1	0	0	1
y4	-20000	-45	-7	-4	0	0	0
	0	0	0	0	0	0	0
y5	-29895	0	7	0	-45	7	-4
	48	0	0	4	0	0	4

bi		x11		x12		x13		x21		y2		y3
-978/5	23	-5	-12/5	58	-10	-19/5
464	-58	0	0	-58	0	0
y1	8	1	0	0	1	0	0
	8	1	0	0	1	0	0
x22	15	0	1	0	0	1	0
	0	0	0	0	0	0	0
x23	12	0	0	1	0	0	1
	0	0	0	0	0	0	0
y4	-20000	-45	-7	-4	0	0	0
	0	0	0	0	0	0	0
y5	-29847	0	7	4	-45	7	4
	360	45	0	0	45	0	0

bi		x11		x12		x13		y1		y2		y3
1342/5	-35	-5	-12/5	-58	-10	-19/5
x21	8	1	0	0	1	0	0
	x22	15	0	1	0	0	1	0
x23		12	0	0	1	0	0	1
	y4	-20000	-45	-7	-4	0	0	0
y5		-29487	45	7	4	45	7	4

Ответ: Задача не имеет допустимого решения

Задача 2

№ вар	с1		с2		с3		с4		с5		с6		b1		b2		b3		Знаки ограничений							a11		a12		a13	a14
																			1		2			3
8	2		6		2		–2		2		0		2		6		1		=		=			=		–1		2		1	0
№ вар.		a15		a16		a21		a22		a23		a24		a25		a26		a31		a32		a33	a34		a35		a36		Тип экстр.
8		0		0		2		1		1		1		2		0		1		–1		0	0		1		0		max

1. Основная задача линейного программирования:

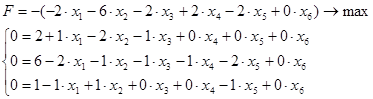
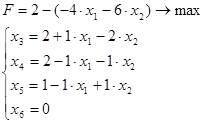
Правую часть уравнений (ограничения и целевую функцию) представляем в виде разности между свободным членом и суммой всех остальных:

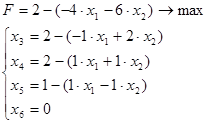
2. Составим симплекс – таблицу:

bi		x1		x2
2	-4	-6
x3	2	-1	2
	x4	2	1	1
x5		1	1	-1

3. Решим задачу линейного программирования.

bi		x1		x2
2	-4	-6
6	-3	3
x3	2	-1	2
	1	-0.5	0.5
x4	2	1	1
	-1	0.5	-0.5
x5	1	1	-1
	1	-0.5	0.5

bi		x1		x3
8	-7	3
21/4	21/4	-21/8
x2	1	-0.5	0.5
	3/8	3/8	-3/16
x4	1	1.5	-0.5
	3/4	3/4	-3/8
x5	2	0.5	0.5
	-3/8	-3/8	3/16

bi		x4		x3
53/4	21/4	3/8
x2	11/8	3/8	5/16
	x1	3/4	3/4	-3/8
x5		13/8	-3/8	11/16

Оптимальное решение найдено.

Ответ: F=53/4, x₁ =3/4, x₂ =11/8, x₃ =0, x₄ =0, x₅ =13/8, x₆ =0.

Задача 3

№ вар.	а1	а2	а3	b1	b2	b3	b4	b5	с11	с12	с13
8	200	200	600	200	300	200	100	200	25	21	20

№ вар.	с14	с15	с21	с22	с23	с24	с25	с31	с32	с33	с34	с35
8	50	18	15	30	32	25	40	23	40	10	12	21

Исходные данные:

B1	B2	B3	B4	B5	аi
A1	25	21	20	50	18	200
A2	15	30	32	25	40	200
A3	23	40	10	12	21	600
bi	200	300	200	100	200	1000

Определение опорного плана задачи

B1	B2	B3	B4	B5	аi
A1	25	21	20	50	18	200
	200
A2	15	30	32	25	40	600
	300	200	100
A3	23	40	10	12	21	200
	200
bi	200	300	200	100	200	600

L=5000+9000+6400+2500+4200=27300

r+m-1=7>5 это вырожденный случай.

Определение оптимального плана