Курсовая работа: Исследование точности численного интегрирования 2
1,93E-07
7,79E-08
1,29E-07
1,17E-07
1,93E-07
7,79E-08
1,29E-07
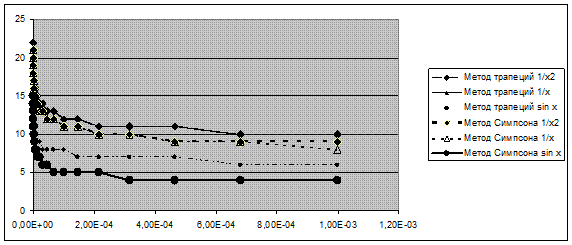
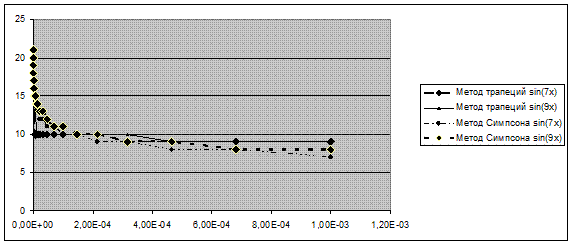
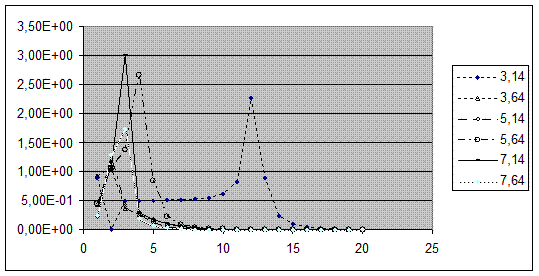
Рисунок 2. Зависимость количества итераций от критерия точности
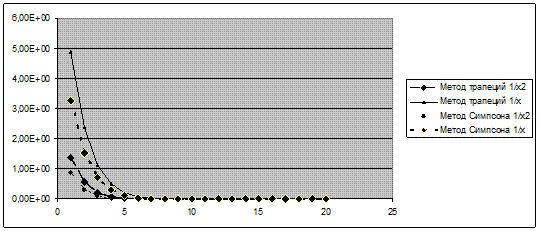
Рисунок 3. Зависимость количества итераций от критерия точности
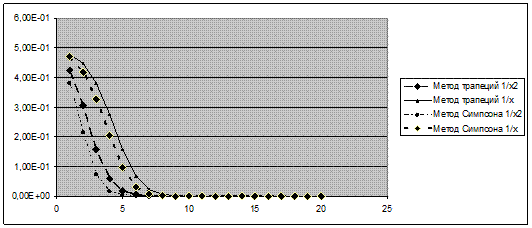
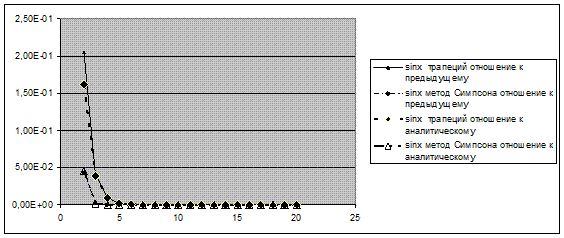
Рисунок 4. Зависимость критерия точности от количества итераций (отношение разности к значению на предыдущей итерации)
Рисунок 5. Зависимость критерия точности от количества итераций (отношение разности к аналитическому значению)
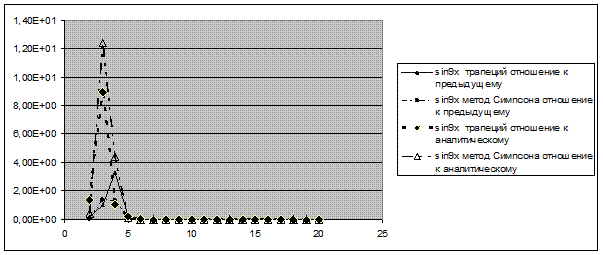
Рисунок 6. Зависимость критерия точности от количества итераций
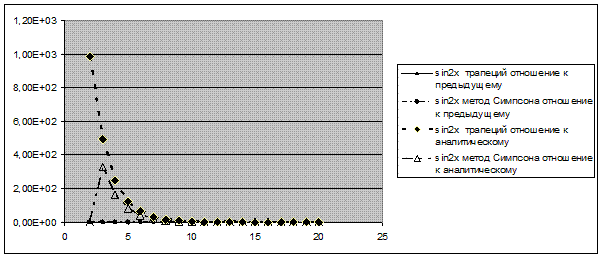
Рисунок 7. Зависимость критерия точности от количества итераций
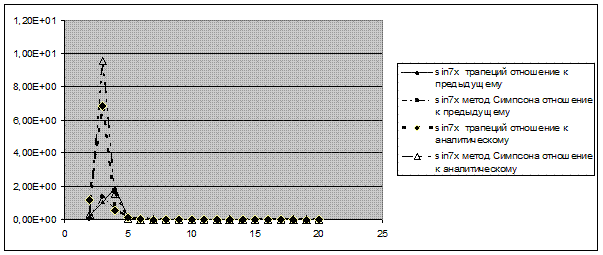
Рисунок 8. Зависимость критерия точности от количества итераций
Рисунок 9. Зависимость критерия точности от количества итераций
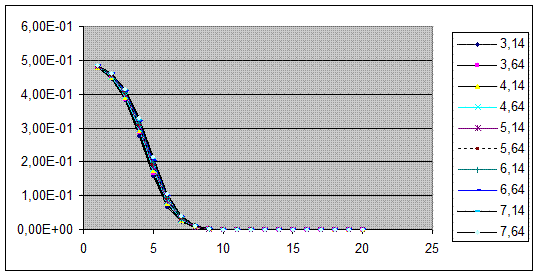
Рисунок 10. Зависимость критерия точности от количества итераций интегрирования 1/х при разных верхних пределах интегрирования.
Рисунок 11
3. Анализ результатов
Если внимательно посмотреть результаты, то можно заметить отсутствие зависимости кол-ва итераций от заданного критерия точности для функции sin2x. Так как исследование проходит на интервале [0, π], то величина данного интеграла равна 0 (то есть в условиях программного расчета близка к нулю). Широко известно, что деление на ноль «не приветствуется», но если проводить расчет в данной программе, то можно увидеть, что в конце концов появится результат – 32 итерации, это происходит из-за того, что кол-во отрезков n, на которые разделен интервал интегрирования, имеет тип int, то есть четырехбайтовое целое знаковое число. На 31 итерации n приняло свой максимум, и на следующих итерациях критерий становится равным 0, что удовлетворяет любому заданному критерию, поэтому я решил, что эти измерения не целесообразны. Из второй зависимости видно что критерий точности для этой функции на двадцатой итерации только начинает приближаться к заданному интервалу критериев точности (порядка 10^-3).
Зависимости для функций 1/ x, 1/x^2, sin7x и sin9x ведут себя почти одинаково при всех данных, а вот sinx отличается относительно «рекордной» точностью в измерениях (особенно расчетом методом трапеций, этот метод лучший при расчете площади под прямой линией).
Интегралы всех функций, кроме sinx, имеют лучшую точность при расчете методом Симпсона, но с учетом, что интервал интегрирования разбит на достаточно большое кол-во отрезков. На первых итерациях данный метод дает точность хуже, так как он рассчитан на более-менее изогнутые и не постоянные функции. Этим же объясняется его «не лучший» расчет интеграла sinx, так как эта функция, по-сравнению с остальными, менее изогнута (на заданном интервале), например sin mx очень часто изгибается, а 1/x и 1/x^2 очень стремительно вначале убывает.
При исследовании на функциях 1/x и sin2x влияния увеличения верхнего предела на точность установлено что, на точность интегрирования функции 1/x увеличение верхнего предела почти не влияет, это видно по графику на рисунке 10.
А вот на функцию sin2x увеличение верхнего предела влияет значительно. При малых значениях итераций с увеличением предела точность ухудшается, а вот при итерациях > 4-5 значительное улучшение.
4. Описание применения
4.1 Назначение программы
Данная программа предназначена для исследования внутренней сходимости численного интегрирования.
4.2 Условия применения.
Программа предъявляет очень скромные требования к ресурсам вычислительной установки. Для компиляции и сборки программы используется Microsoft Visual С++ 2005.
4.3 Описание задачи
Построить зависимости количества итераций от различный величин критерия точности.
Построить обратные зависимости критерия точности от количества итераций.
Повторить все вышеуказанные исследования для случая, когда при вычислении критерия точности разность значений интеграла на смежных итерациях относится не к предыдущему значению, а к точному значению аналитически вычисленного интеграла.
Исследовать влияние увеличения верхнего предела интегрирования на точность (при прочих неизменных величинах).
5. Программа и методика испытаний
5.1 Объект испытаний
Объектом испытаний является программа, предназначенная для исследования внутренней сходимости численного интегрирования с помощью методов вычисления интегралов: методы трапеций и Симпсона.