Курсовая работа: Исследование влияния режимных факторов прессования древесностружечной плиты на разбухание

Разобьем диапазон от 8,111 до 11,085 на интервалы равной длины. Для определения числа интервалов k воспользуемся формулой:

k = 1 + 3,2ln n, (4.1)

где n – объем выборки.

Значение k, найденное по формуле, округляем до ближайшего целого.

k = 1 + 3,2ln 60 7.

Длина каждого интервала:

(4.2)

Предполагается, что выходная величина подчиняется нормальному закону распределения. Это предположение можно проверить разными способами. Наиболее строгим из них является применение критерия χ2 Пирсона. Для этого необходимо иметь выборку достаточно большого объема: n > 50 – 150. Диапазон изменения выходной величины в этой выборке разбивается на l интервалов так, чтобы эти интервалы покрывали всю ось от - до + и в каждый интервал при этом попало не менее пяти значений выходной величины. Подсчитывают количество mi наблюдений, попавших в каждый интервал. Затем вычисляют теоретические попадания случайной величины в каждый i-й интервал. Для этого используют формулу

pi = Ф(z2) – Ф(z1), где (4.3)

z1 = (- ) / s; z2 = ( - ) / s;

где - среднее арифметическое выборки; s – среднее квадратическое отклонение выборки; - нижняя граница i-го интервала; - верхняя граница i-го интервала; Ф(z) – нормированная функция Лапласа:

Ф(z) =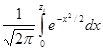

Значения ее для z = z1 и z = z2 определяют из таблиц. При отыскании значений этой функции для отрицательных значений аргумента следует иметь в виду, что функция Ф(z) нечетная:

Ф(- z) = - Ф(z).

Следующим этапом является вычисление величины χ2 по формуле

χ2 = . (4.4)

По выбранному уровню значимости q и числу степеней свободы k = l – 3 из таблицы отыскивают . Гипотезу о нормальности распределения можно принять, если .

Вычисления удобно вести заполняя таблицу:

Таблица 4.2

№ интервала			mi	z1	z2	Ф(z1)	Ф(z2)	pi	pin
1	2	3	4	5	6	7	8	9	10	11	12
1	8,111	8,537	2	-2,19	-2,06	0,014	0,019	0,005	0,3	2,89	9,633
2	8,537	8,963	3	-2,06	-1,18	0,019	0,119	0,1	6	9	1,5
3	8,963	9,389	19	1,18	-0,3	0,119	0,382	0,263	15,78	10,3684	0,657
4	9,389	9,815	18	-0,3	0,58	0,382	0,719	0,337	20,22	4,9284	0,244
5	9,815	10,241	16	0,58	1,46	0,719	0,927	0,208	12,48	12,3904	0,993
6	10,241	10,667	1	1,46	2,34	0,927	0,990	0,063	3,78	7,7284	2,045
7	10,667	11,093	1	2,34	3,22	0,990	0,999	0,009	0,54	0,2116	0,392

Данные выборки разобьем на 7 интервалов, границы которых указаны во втором и третьем столбцах. В четвертом столбце приведено количество наблюдений, попавших в каждый интервал. Далее по данным таблицы 4.1

вычислены среднее и стандарт s выборки.

= =

=

=

=

=

= 9,535