Курсовая работа: Излучение Вавилова-Черенкова

При движении электрона сквозь вещество имеется, конечно, взаимодействие электрона с атомами вещества, в результате, которого часть энергии электрона может предаваться атомам, вызывая их ионизацию или возбуждение. Однако в данном вопросе нас не эти виды потерь энергии электроном. Как показывает детальное рассмотрение электрического поля, создаваемого движущимся электроном, могут иметь место и иные формы растраты энергии электроном. Рассмотрим случай. Пусть электрон со значительной скоростью движется по оси пустотелого канала, проделанного в веществе, так что он не испытывает непосредственных столкновений с атомами вещества. Оказывается, однако, что если диаметр канала значительно меньше длины волны света, то все же электрон теряет энергию в виде световой радиации сквозь поверхность, охватывающую ось цилиндрического канала. При этом мы можем для простоты считать среду вполне прозрачной, так что поток радиации беспрепятственно проходит через нее. Излучаемая энергия, конечно, заимствуется из энергии движущегося электрона, скорость которого должна уменьшиться вследствие торможения электрона в собственном поле. Именно это излучение представляет собой в чистом виде излучение Вавилова-Черенкова.

Расчет показывает, что рассматриваемое излучение и связанное с ним торможение возникают только в том случае, когда скорость электрона больше фазовой скорости света в среде с , и прекращается когда скорость электрона уменьшается до этой скорости. Рассчитав электрическое и магнитное поля движущегося электрона со «сверхсветовой» скоростью электрона и образовав вектор Пойнтинга, можно вычислить поток радиации, излучаемой элктроном.

При этом обнаруживается своеобразное распределениеизлучения в пространстве в идее узкого конического слоя, образующая которого составляет с осью движения угол , так что где - фазовая скорость света; излучение оказывается поляризованным так, что его электрический вектор лежит в плоскости, проходящей через направление движения электрона. Все эти выводы теории оказалась в хорошем соответствии с результатами наблюдения свечения Вавилова-Черенкова.

Наиболее своеобразную особенность рассматриваемого излучения – его угловое распределение и необходимость соблюдения условия можно получить из довольно общих соображений. Представим себе электрон, движущийся со скоростью вдоль линии ОL (рис.1), служащей осью узкого пустотного канала в однородном прозрачном веществе с показателем преломления n . Каждая точка линии OL, последовательно занимаемая электроном, является центром испускания света, но с запозданием, определенным величиной , где а – расстояние между 2 рассматриваемыми положениями электрона. Для того чтобы все волны, исходящие из этих последовательных положений, усиливались в результате взаимной интерференции, необходимо, чтобы разность фаз между ними была равно нулю при любом значении а . из рисунка 1 нетрудно увидеть, что это будет иметь место для направления, составляющего угол с направлением движения электрона, причем определяется из условия:

Откуда .

Действительно, фронт волны, исходящей из О, достигает положения АМ`, где А – новое положение электрона, через время ОМ`/c =: электрон же достигнет точки А через промежуток времени . если указанные промежутки совпадают, , то волна из О и волна из А окажутся в одной фазе, какого бы ни было а .

Итак, мы видим, что направление максимальной интенсивности определиться углом образующей конуса с его осью ОL, удовлетворяющим условию . Если , т.е. скорость ниже фазовой скорости света, то соответствующие направление невозможно. Наоборот, при угол имеет вполне определенное значение, зависящие от скорости электрона и показателя преломления среды в согласии с полной теорией и опытными данными.

Легко видеть также, что если условие не соблюдается, то мы можем всегда разбить траекторию ОL на такие отрезки а , чтобы разность хода между волнами, исходящих из соответствующих двух соседних отрезков (т.е. из точек расположенных на расстоянии а ) была равна . Иными словами, должно выполнятся условие

,

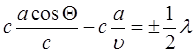Откуда .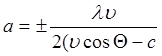

При соблюдении этого условия, свет, исходящий из соответствующих точек соседних участков, будет гаситься вследствие интерференции, и по данному направлению излучение распространяться не будет. Таким образом, единственное направление, по которому в силу взаимной интерференции волн может распространятся излучение, есть направление определяемое условием , имеющим смысл только в случае движения со сверхсветовой скоростью. Конечно, в реальном опыте световой конус не будет бесконечно тонким, ибо поток летящих электронов имеет конечную апертуру и известный разброс скоростей , равно как и показатель преломления n имеет несколько различные значения для разных длин волн видимого интервала. Все это дает более или менее узкий конический слой около направления, определяемого условием .

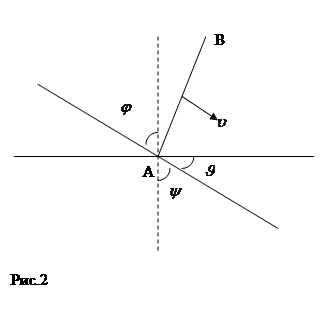
Излучение Вавилова-Черенкова может вызываться не только движущимися частицами, но и каким-либо возбуждением, распространяющимся со скоростью, превышающей фазовую скорость света в среде. Допустим, например, что на границу сред падает волна с плоским фронтом АВ (рис 2). Вдоль границы раздела побежит возмущение со скоростью , где - фазовая скорость света в первой среде. Оно возбудит во второй среде излучение Вавилова-Черенова под углом к границе раздела. Угол определяется из соотношения , где - фазовая скорость света во второй среде. Замечая, что , отсюда находим . 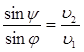Таким образом, преломление света можно трактовать, как эффект Вавилова-Черенкова, возбуждаемый во второй среде падающей волной. Также можно рассматривать и отражение света. В данном случае скорость волнового фронта V совпадает с фазовой скоростью . Отсюда получим, что , т.е. волновой фронт распространяется без изменения направления.

Эффекты, сходные с излучением Вавилова-Черенкова давно известны в гидро- и аэродинамике. Если, например, судно движется по поверхности спокойной воды со скоростью, превышающей, скорость распространения волн на поверхности воды, то возникающие под носом судна волны, отставая от него, образуют плоский конус волн, угол раскрытия которого зависит от соотношения скорости судна и скорости поверхностных волн. При движении снаряда или самолета со сверхзвуковой скоростью возникает звуковое излучение («вой»), законы распространения которого также связаны с образованием так называемого «конуса Маха». Явления эти осложняются сложностью уравнений аэродинамики.

Применения излучения Вавилова-Черенкова

Излучение Вавилова-Черенкова нашло разнообразные применения в экспериментальной ядерной физике и физике элементарных частиц. На нем основано действие так называемых черенковских счетчиков, т.е. детекторов релятивистских заряженных частиц, излучение которых регистрируется с помощью фотоумножителей. Основное назначение черенковских счетчиков – разделение релятивистских частиц с одинаковыми импульсами, но различными скоростями. Пусть, например, пучок, состоящий из релятивистских протонов и -мезонов, проходит через однородное поперечное магнитное поле. Направления траекторий прошедших частиц будут определяться только их импульсами, но не будут зависеть от их скоростей. С помощью диафрагм можно выделить протоны и -мезонов с одинаковыми импульсами. Из-за различия масс скорости -мезонов окажутся несколько больше скоростей протонов . Если полученный пучок направить в газ и подобрать показатель преломления n газа так, чтобы было , то -мезоны будут давать излучение Вавилова-Черенкова, а протоны – нет. Таким образом, счетчик будет регистрировать только -мезоны, но не будет регистрировать протоны.

Несмотря на чрезвычайную слабость свечения, приемники света достаточно чувствительны, чтобы зарегистрировать излучение, порожденное единственной заряженной частицей. Созданы приборы, которые позволяют по излучения Вавилова-Черенкова определить заряд, скорость и направление движения частицы, ее полную энергии. Практически важно применение этого излучения для контроля работы ядерных реакторов.

Список использованной литературы

1. Антонов-Романовский В.В. «Оптика и спектроскопия» 1957г.

2. Степанов Б.И. «Классификация вторичного свечения» 1959г.

3. Принсгейм П. «Флюоресценция и фосфоренценция» 1951г.

4. Левшин В. Л. «Фотолюминесценция жидких и твердых веществ» 1951г.

5. Москвин А. В. «Катодолюминесценция» 1949г.

6. Ландсберг Г.С. «Оптика» 1976 г.

7. Сивухин Д.В. «Курс общей физики. Оптика» 1985 г.

[1] (12 (24) марта 1891, Москва — 25 января 1951, Москва) — советский физик, академик (1932), основатель научной школы физической оптики в СССР, президент Академии наук СССР (с 1945), лауреат Сталинской премии. Младший брат Н. И. Вавилова, русского ученого-генетика

[2] уменьшение выхода люминесценции, вызываемое различными причинами. Тушение люминесценции может происходить при добавлении в люминофор посторонних примесей, при увеличении в нём концентрации самого люминесцирующего вещества (концентрационное тушение), при нагревании (температурное тушение), под действием ИК света, электрического поля и др. воздействий на люминофор.

[3] (28 июля 1904, село Новая Чигла Бобровского уезда Воронежской губернии (ныне Таловский район Воронежской области) — 6 января 1990, Москва) — русский физик, двухкратный лауреат Сталинской премии, лауреат Нобелевской премии по физике (совместно с И. Е. Таммом и И. М. Франком) (1958).

[4] (26 июня (8 июля) 1895, Владивосток — 12 апреля 1971, Москва) — советский физик, лауреат Сталинской премии, лауреат Нобелевской премии по физике (совместно с П. А. Черенковым и И. М. Франком, 1958).