Курсовая работа: Измерение и контроль температуры

Суммарное среднее квадратическое отклонение (с.к.о.) погрешности преобразования:

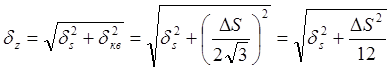; (1.7)

где: - с.к.о. погрешности аналогового сигнала;

- с.к.о. погрешности АЦП за счёт квантования;

∆S - шаг квантования, которому соответствует погрешность .

Здесь 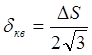, т.к.для входного сигнала принят закон равномерного распределения.

Влияние составляющей, распределённой равномерно, приводит в их композиции к уменьшению доверительных интервалов при заданной доверительной вероятности по сравнению с нормальным законом. Если отношение 0.5∆S/δs=0.1…1.0, то доверительный интервал ±1.7δz имеет доверительную вероятность P=0.98. При отношении 0.5∆S/δs<0.1 при Р=0.99 доверительный интервал будет равен ±2δz.

При отсутствии систематических погрешностей и принятии допущения о том, что случайная погрешность распределена нормально, можно установить зависимость между приведённой допускаемой погрешностью γ и с.к.о. этой погрешности.

При этих условиях 95% значений случайной погрешности находится в пределах от -2δs до +2δs.

Примем

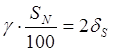; (1.8)

Откуда

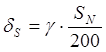; (1.9)

Если с.к.о. погрешности от квантования 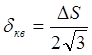принять равным δs,то суммарное с.к.о. в результате квантования согласно (1) увеличивается на 41% по сравнению c δs.

Если принять ∆S=δs, суммарное с.к.о. увеличивается только на 4%,т.е. в этом случае квантование почти не изменит с.к.о. суммарной погрешности. Этому соотношению примерно соответствует минимально допустимое отношение с/d=2, установленное ГОСТ 14014-82 и соответствующее равенству аддитивной и мультипликативной составляющих погрешностей.

Шаг квантования (цена единицы младшего разряда кода)

; (1.10)

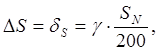(1.11)

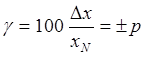; (1.12)

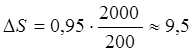
Номинальное число ступеней квантования (разрешающая способность)

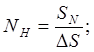(1.13)

Число разрядов кода

(1.14)

Вид кода: двоичный нормальный

Функция преобразования (статическая функция преобразования) - функциональная зависимость между информативными параметрами выходного и входного сигналов.