Курсовая работа: Качественное исследование модели хищник-жертва

2.1 Модель трофического взаимодействия по типу «хищник—жертва»

Рассмотрим модель трофического взаимодействия по типу «хищник—жертва», построенную В. Вольтерром. Пусть имеется система, состоящая из двух видов, из которых один поедает другой.

Рассмотрим случай, когда один из видов является хищником, а другой — жертвой, и будем считать, что хищник питается только жертвой. Примем следующую простую гипотезу:

— коэффициент прироста жертвы;

— коэффициент прироста хищника;

— численность популяции жертвы;

— численность популяции хищника;

— коэффициент естественного прироста жертвы;

— скорость потребления жертвы хищником;

— коэффициент смертности хищника в отсутствие жертвы;

— коэффициент «переработки» хищником биомассы жертвы в собственную биомассу.

Тогда динамика численности популяций в системе хищник — жертва будет описываться системой дифференциальных уравнений 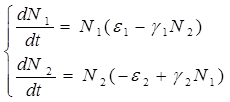(2.1):

(2.1)

где все коэффициенты положительные и постоянные.

Модель имеет равновесное решение 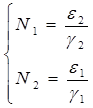(2.2):

(2.2)

По модели (2.1) доля хищников в общей массе животных выражается формулой 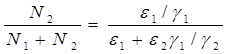(2.3):

(2.3)

Анализ устойчивости состояния равновесия по отношению к малым возмущениям показал, что особая точка (2.2) является «нейтрально» устойчивой (типа «центр»), т. е. любые отклонения от равновесия не затухают, но переводят систему в колебательный режим с амплитудой, зависящей от величины возмущения. Траектории системы на фазовой плоскости имеют вид замкнутых кривых, расположенных на различных расстояниях от точки равновесия (рис. 1).

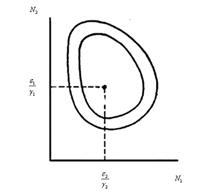
Рис. 1 – Фазовый «портрет» классической вольтерровой системы «хищник-жертва»

Разделив первое уравнение системы (2.1) на второе, получим дифференциальное уравнение (2.4) для кривой на фазовой плоскости .

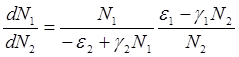(2.4)

Интегрируя данное уравнение получим:

(2.5)

где - постоянная интегрирования, где

Несложно показать, что движение точки по фазовой плоскости будет происходить только в одну сторону. Для этого удобно сделать замену функций и , перенеся начало координат на плоскости в стационарную точку (2.2) и введя затем полярные координаты:

(2.6)

В таком случае, подставив значения системы (2.6) в систему (2.1), будем иметь: