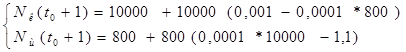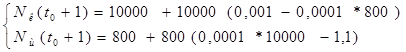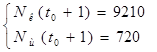Курсовая работа: Качественное исследование модели хищник-жертва

Эта система дифференциальных уравнений в силу ее достаточной общности позволяет хорошо учитывать реальное поведение популяций и вместе с тем проводить качественный анализ ее решений.

Позднее в своей работе, Колмогоров исследовал подробно менее общую модель:

(2.18)

Различные частные случаи системы дифференциальных уравнений (2.18) исследовались многими авторами. В таблице приведены различные частные случаи функций , , .

Таблица 1 - Различные модели сообщества «хищник-жертва»

			Авторы
			Вольтерра-Лотка
			Гаузе
			Пислоу
			Холинг
			Ивлев
			Рояма
			Шимазу
			Мэй

математическое моделирование хищник жертва

3. ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ МОДЕЛИ ХИЩНИК-ЖЕРТВА

Рассмотрим математическую модель совместного существования двух биологических видов (популяций) типа "хищник - жертва", называемую моделью Вольтерра - Лотки.

Пусть два биологических вида совместно обитают в изолированной среде. Среда стационарна и обеспечивает в неограниченном количестве всем необходимым для жизни один из видов, который будем называть жертвой. Другой вид - хищник также находится в стационарных условиях, но питается лишь особями первого вида. Это могут быть караси и щуки, зайцы и волки, мыши и лисы, микробы и антитела и т. д. Будем для определенности называть их карасями и щуками.

Заданы следующие начальные показатели:

Наименование показателя	Щуки	Караси
— начальная численность популяции	10000	800
—коэффициент естественного прироста/смертности	1,1	0,001
—коэффициенты межвидового взаимодействия	0,0001	0,0001

Со временем число карасей и щук меняется, но так как рыбы в пруду много, то не будем различать 1020 карасей или 1021 и поэтому будем считать и непрерывными функциями времени t. Будем называть пару чисел (,) состоянием модели.

Очевидно, что характер изменения состояния (,) определяется значениями параметров. Изменяя параметры и решая систему уравнений модели, можно исследовать закономерности изменения состояния экологической системы во времени.

В экосистеме скорость изменения численности каждого вида также будем считать пропорциональной его численности, но только с коэффициентом, который зависит от численности особей другого вида. Так, для карасей этот коэффициент уменьшается с увеличением числа щук, а для щук увеличивается с увеличением числа карасей. Будем считать эту зависимость также линейной. Тогда получим систему из двух дифференциальных уравнений:

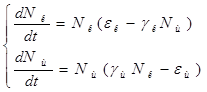
Эта система уравнений и называется моделью Вольтерра-Лотки. Числовые коэффициенты , , - называются параметрами модели. Очевидно, что характер изменения состояния (,) определяется значениями параметров. Изменяя эти параметры и решая систему уравнений модели, можно исследовать закономерности изменения состояния экологической системы.

Проинтегрируем оба уравнения систему по t, которое будет изменяться от - начального момента времени, до , где T – период, за который происходят изменения в экосистеме. Пусть в нашем случае период равен 1 году. Тогда система принимает следующий вид:

;

;

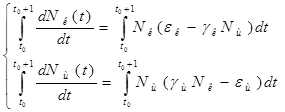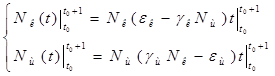Принимая = и = приведем подобные слагаемые, получим систему, состоящую из двух уравнений:

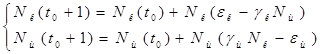
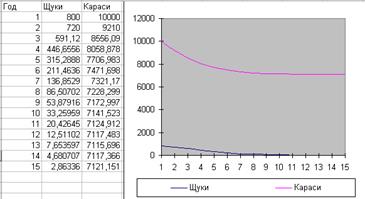
Подставив в полученную систему исходные данные получим популяцию щук и карасей в озере спустя год: