Курсовая работа: Характеристика и применение риск (САРМ, АРТ)
где: βim 1 - бета, рассчитанная относительно портфеля M1
βim 2 - бета, рассчитанная относительно портфеля M2.
2.2 САРМ с нулевой бетой
Вторая модификация САРМ возникает для случая, когда имеется актив, который содержит только нерыночный риск. Рыночный риск у него отсутствует, и поэтому его бета равна нулю. Для такой ситуации можно построить SML, которая будет проходить через рыночный портфель и рискованный актив с нулевой бетой. Уравнение САРМ в этом случае принимает вид
![]()
где: r0 - рискованный актив с нулевой бетой.
В качестве актива с нулевой бетой можно, например, рассматривать облигацию крупной компании. Если инвестор будет держать ее до погашения, то гарантирует себе определенный уровень процента, который не зависит уже от последующих колебаний цены этой бумаги. Единственный риск, которому подвергается вкладчик, это риск банкротства эмитента, поскольку в этом случае предприятие может и не осуществить причитающиеся ему платежи по облигациям.
2.3 Версия САРМ для облигаций
Модель САРМ можно построить для облигаций. Она имеет следующий вид:
![]() (***)
(***)
где: E(ri ) - ожидаемая доходность i-й облигации;
Е(rm ) - ожидаемая доходность рыночного портфеля облигаций;
βi - коэффициент бета i-й облигации. Он равен отношению дюрации облигации i (Di ) к дюрации рыночного портфеля облигаций (Dm ).
Формула (***) говорит: если доходность рыночного портфеля облигаций вырастет на 1%, то доходность i-й облигации возрастет на величину β . На рис. 10 представлена линия рынка облигаций. Как следует из формулы, в данной версии САРМ доходность облигации является линейной функцией дюрации облигации.
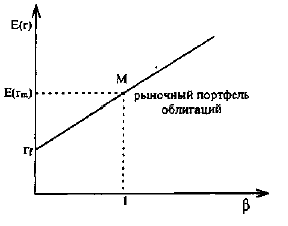
Рис. 10. Линия рынка облигаций
При использовании данной модели следует помнить, что она завышает доходность долгосрочных облигаций при повышении ставок. Так, для облигации с дюрацией 10 лет формула дает результат, который в 10 раз больше, чем для облигации с дюрацией 1 год. На практике данная разница не столь велика.
3. Теоретические и практические аспекты использования модели арбитражного ценообразования (АРТ)
3.1 Общий вид модели арбитражного ценообразования
Теория арбитражного ценообразования (АРТ) была предложена профессором Йельского университета С. Россом в 1976 г. и является альтернативной САРМ моделью общего равновесия на финансовом рынке. Главным предположением теории является то, что каждый инвестор стремится использовать возможность увеличения доходности своего портфеля без увеличения риска. Механизмом, способствующим реализации данной возможности, является арбитражный портфель.
Арбитраж (arbitrage) — это получение безрисковой прибыли путем использования разных цен на одинаковую продукцию или ценные бумаги. Арбитраж, являющийся широко распространенной инвестиционной тактикой, обычно состоит из продажи ценной бумаги по относительно высокой цене и одновременной покупки такой же ценной бумаги (или ее функционального эквивалента) по относительно низкой цене. Арбитражная деятельность является важной составляющей современных эффективных рынков ценных бумаг. Поскольку арбитражные доходы являются безрисковыми по определению, то все инвесторы стремятся получать такие доходы при каждой возможности.
Определить, подходит ли ценная бумага или портфель для арбитражных операций, можно различными способами. Одним из них является анализ общих факторов, которые влияют на курс ценных бумаг. Факторная модель подразумевает, что ценные бумаги или портфели с одинаковыми чувствительностями к факторам ведут себя одинаково, за исключением внефакторного риска. Поэтому ценные бумаги или портфели с одинаковыми чувствительностями к факторам должны иметь одинаковые ожидаемые доходности, в противном случае имелись бы "почти арбитражные" возможности. Но как только такие возможности появляются, деятельность инвесторов приводит к их исчезновению.
Теория арбитражного ценообразования утверждает, что ожидаемая доходность отдельной ценной бумаги зависит от множества разнообразных факторов, а не от одного интегрированного рыночного фактора, отражаемого классической Моделью САРМ. В качестве таких факторов он рассматривает все виды систематичсеких рисков раздельно, предлагая компенсировать каждый из факторов риска в процессе оценки стоимости финансового актива (ценной бумаги). При наличии n таких независимых
Модель теории арбитражного ценообразования имеет следующий вид:
Дфа = Дб/р + β1 (Дрп1 – Дб/р ) + + β2 (Дрп2 – Дб/р ) +…++ βn (Дрп n – Дб/р ),
β1 … βn - коэффициент "бета", измеряющий чувствительность рассматриваемого финансового актива к фактору 1…n;
Дрп1 …Дрп n – уровень ожидаемой доходности рыночного портфеля, компенсирующий данный вид риска (фактора);
n – общее количество рассматриваемых факторов, систематически влияющих на уровень доходности отдельных финансовых активов и рыночного портфеля в целом.
Арбитражная теория ценообразования позволяет существенно сократить число ограничительных предложений, принятых при построении классической модели оценки стоимости финансовых активов, что усиливает возможность ее практического использования.
Модель АРТ обычно сравнивают с моделью САРМ. С теоретической точки зрения модель АРТ обладает неоспоримыми преимуществами:
- Модель АРТ расщепляет факторы риска на составляющие, приближая их к условиям, в которых действует конкретный бизнес;
- АРТ использует относительно более слабые упрощающие анализ предположения по сравнению с моделью оценки капитальных активов САРМ.
Однако у модели АРТ есть и свои недостатки, а именно: