Курсовая работа: Конструкция и методика расчёта шахтных печей цветной металлургии

При Wг = Wм и dТг = dТм охлаждение газов на 1 °С обеспечивает нагрев металла также на 1 0С. Следовательно, на всей высоте слоя разность температур между Тг и Тм будет одинаковой, что обеспечивает прямолинейный характер изменения этих температур по высоте слоя.

Если Wг < Wм, то при достаточной поверхности нагрева газы отдадут все свое тепло материалу (Т''г и Т'м), однако этого тепла не хватит, чтобы

нагреть материал до начальной температуры газов.

Как будет показано ниже, в разных частях шахтной печи возможны случаи, когда Wг > Wм и Wм > Wг, поэтому рассмотрим подробнее теплообмен при Wг > Wм сначала для случая термически тонких кусков. С этой целью выделим элементарный участок слоя, через который в единицу времени прохо­дит объем материала Vм с поверхностью F.

Количество тепла, переданное материалу, может быть записано следующим образом:

, (3)

где α — коэффициент теплоотдачи от газов к поверхности кусков, Вт/(м2 ∙ К).

При отсутствии тепловых потерь для противотока характерно, что в любом сечении по высоте слоя (рисунок 1).

, (4)

откуда (5)

Подставив выражение (5) в уравнение (3), можно получить после соответствующих преобразований неходкое дифференциальное уравнение

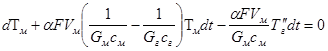(6)

решением которого будет

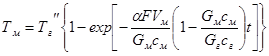(7)

Из последнеговыражения следует, что при t=∞ (высота слоя ∞) температура кусков материала на выходе из слоя Т''м достигнет температуры газов на входе в слоя Т'г. Если учесть, что для этого момента времени Т'г ≈ Т''м, то из выражения (5) можно получить:

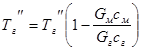(8)

Учитывая, что αv=αF, t = H/p и Gм cм /Vм = cм pнас (pнас – плотность насыпного слоя) и, перейдя к безразмерной форме, можно записать следующее выражение для условий завершенного теплообмена (Т'г ≈ Т''м) при Wг > Wм:

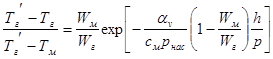(9)

Приведенные выше выражения устанавливают связь между всеми основными величинами, определяющими изменение температуры материала в слое и температуры газов.

Для случая Wм > Wг, аналогичные рассуждения приводят к выражению:

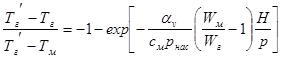
Уместно напомнить, что все вышеприведенные рассуждения относятся к нагреву кусков, представляющих собой термически тонкие тела, т. е. без учета внутреннего теплообмена в кусках. В действительности реальные куски могут не быть термически тонкими телами, т. е. не будет иметь место равенство , где , — время прогрева кусков соответственно с реальной и с бесконечно большой теплопроводностью. Для реальных кусков можно говорить о какой-то условной величине отношения / , которое будет зависеть от критерия Bi . Поскольку куски бесформенны, то для них практически невозможно определить точно величину линейного размера, входящего в критерий Bi. Если с определенной степенью приближения считать, что куски имеют форму шара, то

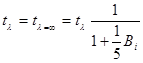
где Bi = ; R – радиус шара.

После соответствующей подстановки в уравнение (7) можно получить выражение

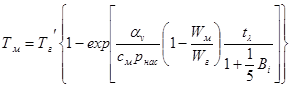
которое позволяет делать необходимые расчеты нагрева слоя, состоящего реальны кусков.

Bo все приведенные выражения, естественно, входят величины коэффициентов теплоотдачи, которые определяются экспериментальным путем.

Большой практический интерес представляет определение гидравлического сопротивления слоя. Хаотическое распределение кусков неопределенность сечений для прохода газов - все это делает возможным, по существу, лишь эмпирический путь исследования этих вопросов. В результате неопределенности формы и размеров пор между кусками определения отдельных элементов местных сопротивлений выполнить невозможно, поэтому они учитываются общим коэффициентом Ксл, входящим в нижеприведенную формулу для определения потерь напора в слое, Па: